[DataScience][Study] 데이터 과학을 위한 통계 1-2
Chapter 1 탐색적 데이터 분석
1.4 변이 추정
- 위치는 데이터의 특징을 요약하는 다양한 요소들 중 하나.
-
두번째 요소인 변이는 데이터가 얼마나 밀집해 있는지 혹은 퍼져 있는지 나타내는 산포도를 나타낸다.
- 용어정리
- 편차 (deviation) : 관측값과 위치 추정값 사이의 차이
- 분산(variance) : 평균과 편차를 제곱한 값들의 n-1로 나눈 값, n은 데이터 갯수
- 표준편차 (standard deviation) : 분산의 제곱근
- 평균 절대 편차 : 평균과 편차의 절댓값의 평균
- 중간값의 중위 절대 편차 : 중간값과의 편차의 절댓값의 중간값
- 범위 : 데이터의 최댓값과 최솟값 차이
- 순서 통계량 : 최소에서 최대까지 정렬된 데이터 값에 따른 계량형
- 백분위수 : 어떤 값들이 p 퍼센트가 이값 혹은 더 작은 값을 갖고 (100-p)퍼센트가 이값 혹은 더 큰값을 가지는 것.
- 사분위범위 : 75번째 백분위수와 25번째 백분위수 사이의 차이
1.4.1 표준편차와 관련 추정값들
- 편차 : 데이터가 중앙값을 주변으로 얼마나 퍼져 있는지 말해준다.
- 표준편차는 원래 데이터와 같은 척도에 있기때문에 분산보다 훨씬 해석하기 쉽다.
- 분산, 표준편차, 평균절대편차 모두 특잇값과 극단값에 로버스트하지않다.
- 분산 표준편차는 제곱 편차를 사용하기 때문에 특히 특잇값에 민감하다.
- 로버스트한 변위 추정값으로는 중간값으로부터의 중위절대편차가 있다.
1.4.2 백분위수에 기초한 추정
- 데이터가 얼마나 퍼져있는지 확인하여 변이 추정.
- 정렬(순위) 데이터를 나타내는 통계량을 순서통계량이라고 부름.
1.4.3 예제 : 주별 인구의 변위 추정
> sd(state[["Population"]])
[1] 6848235
> IQR(state[["Population"]])
[1] 4847308
> mad(state[["Population"]])
[1] 3849870
- 표준편차는 MAD의 거의 두배가 됨. 표준편차는 특잇값에 민감하기 때문.
1.5 데이터 분포 탐색하기
용어정리
- 상자그림 (boxplot) : 데이터 분포를 시각하기 위한 간단한 방법으로 소개
- 도수 분포표 : 어떤 구간에 해당하는 수치 데이터 값들의 빈도를 내타내는 기록
- 히스토그램 : x축은 구간들을, y 축은 빈도수를 나타냄
- 밀도그림 : 히스토그램을 더 부드럽게 표현
1.5.1 백분위수와 상자그림
- 백분위수
> quantile(state[["Murder.Rate"]], p=c(.05, .25, .5, .75, .95))
5% 25% 50% 75% 95%
1.600 2.425 4.000 5.550 6.510
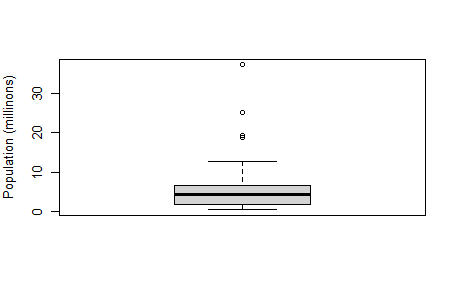
- 상자그림
boxplot(state[["Population"]]/1000000, ylab = "Population (millinons)")
1.5.2 도수분포표와 히스토그램
-
도수 분포표 : 범위를 동일한 크기의 구간으로 나눈 다음, 각 구간마다 몇개의 변수 값이 존재하는지 보여주기 위해 사용.
# 인구의 최솟값과 최댓값 사이를 10개 구간으로 나눈다. breaks <- seq(from = min(state[["Population"]]), to = max(state[["Population"]]), length=11) # 나눈 기준으로 도수 분포표로 데이터 구간을 자른다. pop_freq <- cut(state[["Population"]], breaks = breaks, right = TRUE, include.lowest = TRUE) # 테이블 형태로 출력한다. table(pop_freq)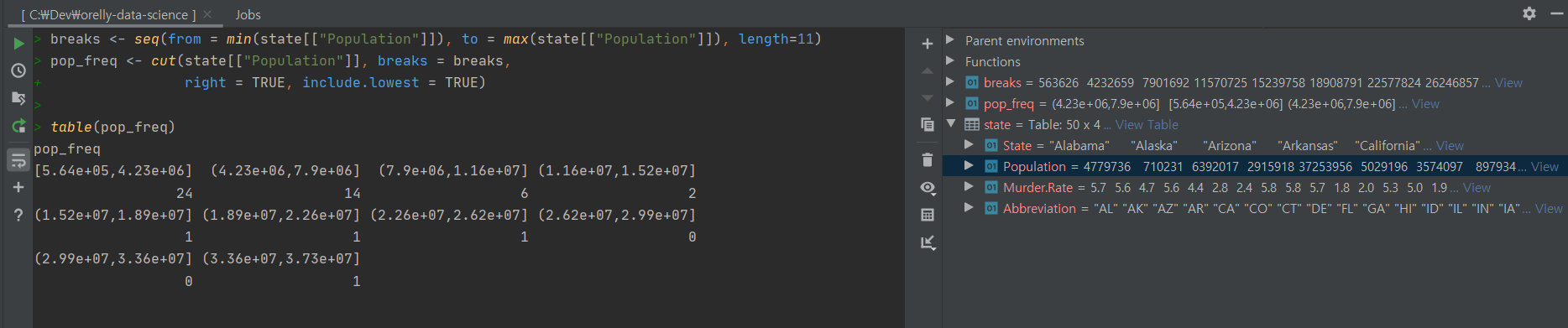
-
히스토그램
- x축에는 구간들을 표시하고, y축에는 해당 구간별 데이터의 개수를 표시.
hist(state[["Population"]], breaks = breaks)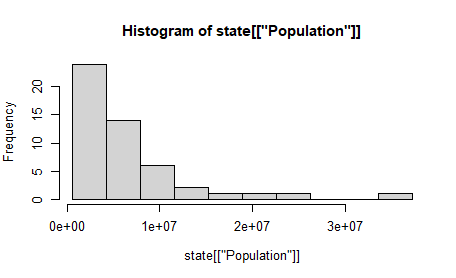
- 특징
- 그래프에 빈 구간들이 있을수 있음
- 구간은 동일한 크기
- 구간의 수(크기)는 사용자가 정할 수 있음
- 빈 구간이 있지 않는 이상, 막대 사이는 공간 없이 서로 붙어 있음.
1.5.3 밀도 추정
-
밀도 그림 : 더 부드러운 히스토그램, 데이터의 분포를 연속 선에서 보여줌.
-
커널 밀도 추정을 통해 데이터로 부터 직접 계산
-
R의 density 함수 사용
hist(state[["Murder.Rate"]], freq = FALSE) lines(density(state[["Murder.Rate"]]), lwd = 3, col = "blue")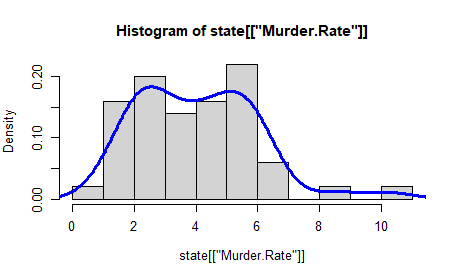
-
히스토그램과의 큰 차이는 y 축 값의 단위가 배율로 표시됨.(히스토그램은 개수 )
1.6 이진 데이터와 범주 데이터 탐색하기
-
범주형 데이터는 간단한 비율이나 퍼센트를 통해 분석
-
용어 정리
- 최빈값 : 데이터의 빈도 수
- 기댓값 : 범주에 해당하는 수치가, 범주에 출현 확률에 따른 평균
- 막대도표 : 각 범주의 빈도수 혹은 비율을 막대로 나타냄
- 파이그림 : 각 범주의 빈도수 혹은 비율을 원의 부채꼴 모양으로 나타냄
-
사례 : 2010년 이후 댈러스-포트워스 공하에서 항공기 운행 지연 원인
-
R의 barplot 함수 사용
barplot(as.matrix(dfw)/6, cex.axis = .5)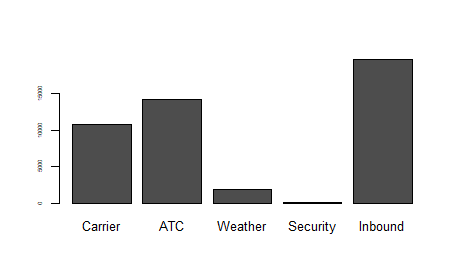
-
막대 도표에서 x축은 각 요인의 변수, 수치적으로 나타낼 수 도 있음.
-
-
파이 도표는 시각적으로 효과적이지 않기 때문에 통계학자나 데이터 시각화 전문가들은 잘 사용하지 않음.
1.6.1 최빈값
- 자주 등장하는 값.
- 범주형 데이터를 분석하는데 사용
- 수치형은 잘 사용되지 않음.
1.6.2 기댓값
- 기댓값은 가중 평균과 같음
- 보통 주관적인 평가에 따른 미래의 기댓값과 각 확률 가중치만큼을 모두 더한 값.
참고 : 해당 포스트의 내용은 O’REILLY 시리즈
데이터 과학을 위한 통계( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.
댓글남기기