[DataScience][Study] 데이터 과학을 위한 통계 1-3
Chapter 1 탐색적 데이터 분석
1.7 상관관계
- X : 원인, 독립변수 / Y : 결과, 종속 변수
- 양의 상관 관계 : X가 커지면 Y도 커짐, X가 작아지면 Y도 작아짐 , 비례
-
음의 상관 관계 : X가 커지면 Y는 작아짐, X가 작아지면, Y는 커짐, 반비례
-
용어정리
-
상관계수 : 수치적 변수들 간에 어떤 관계가 있는지 사용되는 측정량 (-1~ 1)
- 피어슨 상관계수라고도 부르는 표준화된 방식
- 두 변수 사이의 상관관계를 항상 같은 척도에 놓고 추정.
- +1 : 완전한 양의 상관관계
- -1 : 완전한 음의 상관관계
- 0 : 아무런 상관성이 없다.
- 변수들이 선형적인 관계를 갖지 않을 경우엔 유용하지 않음.
-
상관 행열: 행과 열로 상관계수 값을 나타냄
-
R의 corrplot 패키지 사용
# 파일 다운로드 sp500_px <- read.csv(file = 'source/sp500_px.csv') sp500_sym <- read.csv(file = 'source/sp500_sym.csv', stringsAsFactors = FALSE) # 데이터 보기 # head(sp500_sym) # 상관관계 라이브러리 다운로드 install.packages("corrplot") library(corrplot) # 2012-07-01 이후 데이터 기준으로 주식 상장 항목의 상관계수 생성 etfs <- sp500_px[row.names(sp500_px) > "2012-07-01", sp500_sym[sp500_sym$sector=="etf", 'symbol']] # 상관 행열 생성 corrplot(cor(etfs), method = "ellipse")
QQQ 와 XLK경우 양의 상관관계를 보인다.
GLD, USO, VXX는 음의 상관관계를 보인다.
타원의 색깔과 너비는 상관관계의 강도를 의미한다. 얇고 진할수록 더 강한 관계성을 나타낸다.
-
상관관계는 특이점에 예민한다. 그러므로 절사 평균을 사용하여 구한다. R에서는 trim이라는 인수를 제공한다.
-
-
산점도 : x축과 y 축이 서로 다른 두 개의 변수를 나타내는 도표
-
1.7.1 산점도
-
두 변수 사이의 관계를 시각화 하는 기본적인 방법
-
x,y축은 각각의 변수들을 의미하고 그래프의 각 점은 하나의 레코드를 의미함.
> telecom <- sp500_px[, sp500_sym[sp500_sym$sector=="telecommunications_services", 'symbol']] > head(telecom) T CTL FTR VZ LVLT 1 -0.21626771 -0.46391947 0.00000000 -0.06407607 0 2 0.09611898 0.17397279 0.01449721 0.14951282 0 3 0.07208924 0.08698639 0.02899756 0.08543676 0 4 0.00000000 0.00000000 -0.02899733 0.10679658 0 5 -0.04805949 0.28995152 0.02899756 -0.10679231 0 6 -0.06007437 0.08698638 -0.04349768 -0.06407625 0위의 telecom 데이터의 산점도를 출력한다.
plot(telecom$T, telecom$VZ, xlab = "T", ylab = "VZ")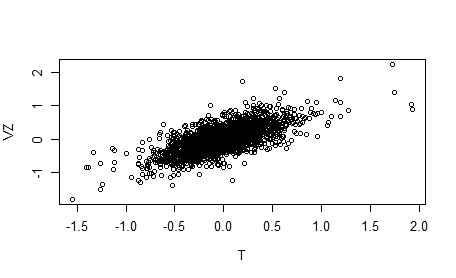
산점도를 분석하면 두 회사의 수익은 강한 양의 상관성을 보인다.
1.8 두개 이상의 변수 탐색하기
-
변수의 갯수에 따라 일변량 분석, 이변량 분석, 다변량 분석으로 나뉨.
- 이변량 분석 역시 요약 통계를 계산하고 시각화를 기본으로 함.
-
이변량 분석 혹은 다변량 분석의 형태는 데이터가 수치형인지 범주형인지 데이터의 특성에 따라 달라짐.
- 용어정리
- 분할표 : 두 가지 이상의 범주형 변수의 빈도수를 기록한 표
- 육각형 구간 : 두 변수를 육각형 모양으로 구간으로 나눈 그림
- 등고 도표 : 지도상에 같은 높이의 지점을 등고선으로 나타내는 것처럼, 두변수의 밀도를 등고선으로 표시한 도표
- 바이올린 도표 : 상자그림과 비슷하지만 밀도 추정을 함께 보여줌.
1.8.1 육각형 구간과 등고선(수치형 변수 대 수치형 변수를 시각화)
-
산점도는 데이터의 개수가 상대적으로 적을때 적합.
-
데이터의 개수가 많으면 너무 밀집되어 알아보기 어렵기 때문에 subset 함수를 이용해 제거.
> kc_tax <- read.csv(file= 'source/kc_tax.csv') > head(kc_tax) TaxAssessedValue SqFtTotLiving ZipCode 1 NA 1730 98117 2 206000 1870 98002 3 303000 1530 98166 4 361000 2000 98108 5 459000 3150 98108 6 223000 1570 98032 > kc_tax0 <- subset(kc_tax, TaxAssessedValue < 750000 & SqFtTotLiving > 100 & SqFtTotLiving < 3500) > head(kc_tax0) TaxAssessedValue SqFtTotLiving ZipCode 2 206000 1870 98002 3 303000 1530 98166 4 361000 2000 98108 -
육각형 구간 그림은 점으로 표시하는 대신 기록값들을 육각형 모양의 구간들로 나누고 각 구간에 표함된 기록값의 개수에 따라 색깔을 표시함.
-
R의 ggplot2패키지를 이용하여 육각형 구간 도표 그래프 출력
# ggplot을 활용하여 육각형 구간 도표 그래프 출력 ggplot(kc_tax0, (aes(x=SqFtTotLiving, y=TaxAssessedValue))) + stat_binhex(colour="white")+ theme_bw() + scale_fill_gradient(low="white", high = "black")+ labs(x="Finished Square Feet", y="Tax Assessed Value")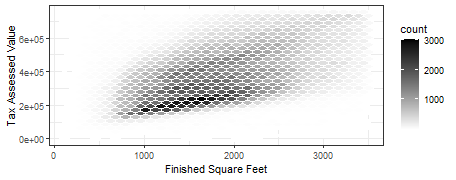
-
R의 ggplot2패키지를 이용하여 등고선 그래프 출력
ggplot(kc_tax0, aes(SqFtTotLiving,TaxAssessedValue )) + + theme_bw() + + geom_point(alpha=0.1)+ + geom_density2d(colour = "white") + + labs(x="Finished Square Feet", y="Tax Assessed Value")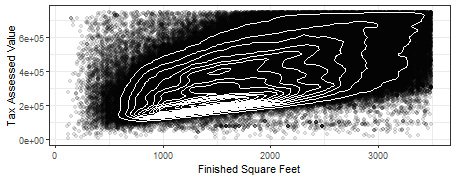
PS. 시간이 조금 오래 걸릴수 있으니 차분히 기다려보자!
1.8.2 범주형 변수 대 범주형 변수
-
분할표는 두 범주형 변수를 요약하는데 효과적
-
범주별 빈도수를 기록한 표를 뜻함.
-
R에서 descr 패키지에서 CrossTable 함수를 활용하면 됨.
> library("descr") > x_tab <- CrossTable(lc_loans$grade, lc_loans$status, + prop.c = FALSE, prop.chisq = FALSE, prop.t = FALSE) > x_tab Cell Contents |-------------------------| | N | | N / Row Total | |-------------------------| ===================================================================== lc_loans$status lc_loans$grade Charged Off Current Fully Paid Late Total --------------------------------------------------------------------- 0.2 146 661 216 63 1086 0.134 0.609 0.199 0.058 0.002 --------------------------------------------------------------------- 0.4 96 524 138 42 800 0.120 0.655 0.172 0.052 0.002 --------------------------------------------------------------------- 0.6 63 360 101 45 569 0.111 0.633 0.178 0.079 0.001 --------------------------------------------------------------------- 0.8 51 228 100 32 411 0.124 0.555 0.243 0.078 0.001 --------------------------------------------------------------------- 1 53 217 88 17 375 0.141 0.579 0.235 0.045 0.001 --------------------------------------------------------------------- 1.2 400 2598 686 161 3845 0.104 0.676 0.178 0.042 0.009 --------------------------------------------------------------------- 1.4 333 1875 576 140 2924 0.114 0.641 0.197 0.048 0.006 --------------------------------------------------------------------- 1.6 302 1748 448 134 2632 0.115 0.664 0.170 0.051 0.006 --------------------------------------------------------------------- 1.8 267 1309 347 91 2014 0.133 0.650 0.172 0.045 0.004 --------------------------------------------------------------------- 2 224 914 271 80 1489 0.150 0.614 0.182 0.054 0.003 --------------------------------------------------------------------- 2.2 597 6401 1435 299 8732 0.068 0.733 0.164 0.034 0.019 --------------------------------------------------------------------- 2.4 670 6011 1470 301 8452 0.079 0.711 0.174 0.036 0.019 --------------------------------------------------------------------- 2.6 561 4798 1186 256 6801 0.082 0.705 0.174 0.038 0.015 --------------------------------------------------------------------- 2.8 547 4066 1001 251 5865 0.093 0.693 0.171 0.043 0.013 --------------------------------------------------------------------- 3 467 3363 857 267 4954 0.094 0.679 0.173 0.054 0.011 --------------------------------------------------------------------- 3.2 1095 13553 3380 533 18561 0.059 0.730 0.182 0.029 0.041 --------------------------------------------------------------------- 3.4 1138 11706 3157 475 16476 0.069 0.710 0.192 0.029 0.037 --------------------------------------------------------------------- 3.6 989 10307 2651 427 14374 0.069 0.717 0.184 0.030 0.032 --------------------------------------------------------------------- 3.8 962 9801 2433 460 13656 0.070 0.718 0.178 0.034 0.030 --------------------------------------------------------------------- 4 823 7914 2060 413 11210 0.073 0.706 0.184 0.037 0.025 --------------------------------------------------------------------- 4.2 1306 18628 5601 525 26060 0.050 0.715 0.215 0.020 0.058 --------------------------------------------------------------------- 4.4 1252 18740 5295 547 25834 0.048 0.725 0.205 0.021 0.057 --------------------------------------------------------------------- 4.6 1175 18234 4348 564 24321 0.048 0.750 0.179 0.023 0.054 --------------------------------------------------------------------- 4.8 1164 17451 4086 570 23271 0.050 0.750 0.176 0.024 0.052 --------------------------------------------------------------------- 5 1126 15875 3817 571 21389 0.053 0.742 0.178 0.027 0.047 --------------------------------------------------------------------- 5.2 664 16132 5066 256 22118 0.030 0.729 0.229 0.012 0.049 --------------------------------------------------------------------- 5.4 863 18390 6099 372 25724 0.034 0.715 0.237 0.014 0.057 --------------------------------------------------------------------- 5.6 1297 21335 7584 458 30674 0.042 0.696 0.247 0.015 0.068 --------------------------------------------------------------------- 5.8 1313 20871 6810 514 29508 0.044 0.707 0.231 0.017 0.065 --------------------------------------------------------------------- 6 1165 17124 5601 456 24346 0.048 0.703 0.230 0.019 0.054 --------------------------------------------------------------------- 6.2 116 7367 2839 38 10360 0.011 0.711 0.274 0.004 0.023 --------------------------------------------------------------------- 6.4 176 7305 3147 43 10671 0.016 0.685 0.295 0.004 0.024 --------------------------------------------------------------------- 6.6 254 8170 3627 60 12111 0.021 0.675 0.299 0.005 0.027 --------------------------------------------------------------------- 6.8 467 12345 5433 144 18389 0.025 0.671 0.295 0.008 0.041 --------------------------------------------------------------------- 7 549 14864 5362 184 20959 0.026 0.709 0.256 0.009 0.046 --------------------------------------------------------------------- Total 22671 321185 97316 9789 450961 =====================================================================
1.8.3 범주형 변수 대 수치형 변수
-
상자그림은 범주형 변수에 따라 분류된 수치형 변수의 분포를 시각화하여 비교함.
- 데이터의 특잇값을 명확하게 보여준다.
boxplot(pct_carrier_delay ~ airline, data= airline_stats, ylim=c(0,50))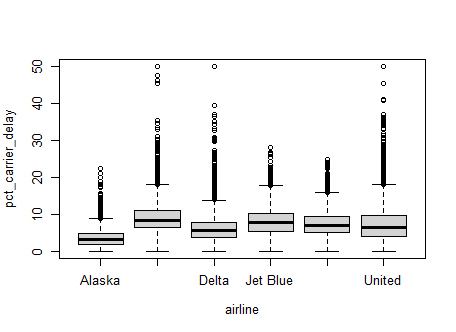
-
바이올린 도표는 상자 그림을 보완한 형태로 y축을 따라 밀도 추정 결과를 동시에 시각화 함.
- 상자 그림에서 보이지 않는 데이터 분포를 볼 수 있다.
- ggplot2에서 geon_violin 함수를 이용하여 도표 생성.
ggplot(data = airline_stats, aes(airline, pct_carrier_delay))+ ylim(0,50) + geom_violin() + labs(x="", y="Daily % of Delay Flights")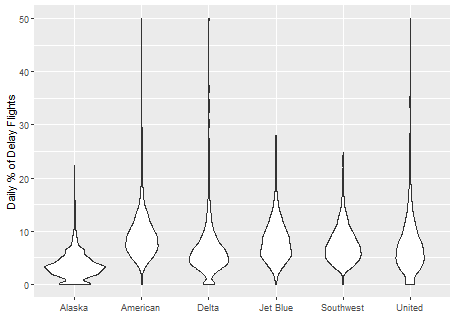
- 델타 항공이 거의 0 근처에 데이터가 집중되어 있다.
1.8.4 다변수 시각화하기
-
조건화라는 개념을 통해 두 변수 비교용 도표(산점도, 육각형 구간, 상자 그림)를 더 여러 변수를 비교하는 용도로 확장하여 활용.
-
facets 라는 조건화 변수 개념을 사용함
ggplot(subset(kc_tax0, ZipCode %in% c(98188, 98105, 98108, 98126)), aes(x=SqFtTotLiving, y=TaxAssessedValue)) + stat_binhex(colour="white") + theme_bw() + scale_fill_gradient( low="white", high="black") + labs(x="Finished Square Feet", y="Tax Assessed Value") + facet_wrap("ZipCode")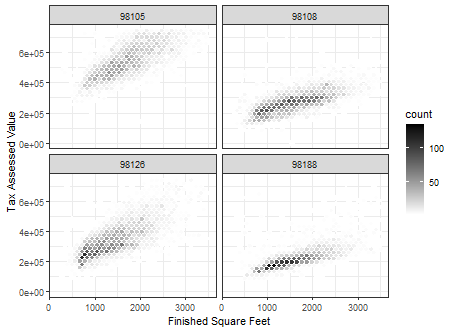
-
참고 : 해당 포스트의 내용은 O’REILLY 시리즈
데이터 과학을 위한 통계( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.
댓글남기기