[DataScience][Study] 데이터 과학을 위한 통계 2-1

---

Chapter 2 데이터와 표본 분포

• 빅데이터 : 결국 작은 표본(샘플) 데이터를 가지고, 예측 모델을 개발하고 테스트한다.
• 샘플은 다양한 종류의 테스트에도 사용(예: 가격 정책이나 웹 트리트먼트)
• 표본 추출 : 모집단에서 샘플 데이터를 얻어내는 절차.

2.1 랜덤표본추출과 표본편향

• 표본 : 큰 데이터(모집단) 집합으로부터 얻은 데이터의 부분 집합.

• 모집단 : 어떤 데이터 집합을 구성하는 전체 대상 혹은 전체 집합.

• 랜덤표본추출 : 대상이 되는 모집단 내의 선택 가능한 원소들을 무작위로 추출하는 과정, 각 추첨에서 모든 원소는 동일한 확률로 뽑히게 된다. 그 결과로 얻은 샘플을 단순랜덤표본이라고 부름.

• 복원 추출 : 추첨 후 다음 번에 중복 추출이 가능하도록 해당 샘플을 다시 모집단에 포함 시키는 것.

• 비복원 추출 : 추첨 후 한번 뽑힌 원소는 추후 추첨에 사용하지 않는 것.

• 표본 편향 : 원래 대표되도록 의도된 모집다능로부터 추출되지 않고 유의미한 비임의 방식으로 표본이 추출된 것

  • 비임의 (nonrandom) : 아무리 랜덤 표본이라고 해도 어떤 표본도 모집단을 정확하게 대표할 수 없다.

2.1.1 편향

• 통계적 편향 : 측정 과정 혹은 표본추출 과정에서 발생하는 계통적인 오차를 의미.
• 랜덤표본추출로 인한 오류와 편향에 따른 오류는 신중하게 구분해서 봐야 함.

2.1.2 랜덤 선택

• 접근 가능한 모집단의 적절한 정의가 매우 중요함.
• 사례 : 고객의 대표 프로필을 만들 목적으로 파일럿 고객 설문 조사 준비

2.1.3 크기와 품질: 크기는 언제 중요해질까?

• 데이터의 개수가 중요해지는 경우가 있음.
• 랜덤표본 추출을 통해 편향을 줄이고 데이터 탐색 및 데이터 품질에 더 집중함.
• 구글의 검색 쿼리 : 주어진 쿼리에 대해 가장 잘 예측 된 검색 대상을 결정하는 것.
• 현대 검색 기술의 진정한 가치는 백만 번에 한 번 정도 발생하는 검색 쿼리까지도 포함하여 다양한 검색 쿼리에 대해서 상세하고 유용한 결과를 얻을 수 있다.

2.1.4 표본평균과 모평균

• 기호 -(엑스 바)는 모집단의 표본 평균을 나타내는 데 사용
• 모집단의 평균은 μ 로 표기.

2.2 선택 편향

• 선택편향 : 데이터를 의식적이든 무의식적이든 선택적으로 고르는 관행을 의미함.
• 방대한 검색 효과 : 큰 데이터 집합을 가지고 반복적으로 다른 모델을 만들고 다른 질문을 하다보면 언젠간 흥미로운 것을 발견하게 된다.
• 이러한 것을 방지하기 위해 홀드아웃 세트나 목푯값 섞기(순열 검정)을 추천함

2.2.1 평균으로의 회귀

• 주어진 어떤 변수를 연속적으로 추정했을 때 나타나는 현상.

• 평균에 대한 회귀는 일조으이 선택 편향으로 인해 나타나는 결과이다.

• 선형회귀와는 구분되어야하는 개념이다.

  • 선형회귀 : 예측변수와 결과 변수와의 관계.

2.3 통계학에서의 표본분포

• 통계의 표본분포라는 용어는 하나의 동일한 모집단에서 얻은 여러 샘플에 대한 표본통계량의 분포를 나타냄.

• 일반적으로 어떤것을 측정하거나, 뭔가를 모델링하기 위해 표본을 뽑음.
  • 고전 통계에서는 대부분 (작은)표본을 가지고 (매우 큰)모집단을 추론하는 것과 관련이 있음.
• 표본의 변동성 : 어떤 표본을 뽑느냐에 따라서 결과가 달라질 수 있음.

• 평균과 같은 표본 통계량의 분포는 데이터 자체의 분포보다 규칙적이고 종 모양일 가능성이 높음.

• ggplot2을 활용한 히스토 그램

  > # 행열을 변경하여 가져옴
  > loans_income <- read.csv(file ='source/loans_income.csv')[,1]
  > head(loans_income)
  [1]  67000  52000 100000  78762  37041  33000
  > 
  > library(ggplot2)
  > # 단순 랜던표본을 하나 취한다.
  > samp_data <- data.frame(income=sample(loans_income, 1000),
  +                       type = 'data_list')
  > 
  > head(samp_data)
    income      type
  1  64000 data_list
  2  84000 data_list
  3  40000 data_list
  4  58000 data_list
  5  55000 data_list
  6  87000 data_list
  > 
  > # 5개의 값의 평균으로 이뤄진 표본을 하나 생성한다
  > samp_data_5 <- data.frame(
  +               income = tapply(sample(loans_income, 1000*5),
  +                            rep(1:1000, rep(5,1000)), FUN=mean),type='mean_of_5')
  > head(samp_data_5)
     income      type
  1 56220.2 mean_of_5
  2 64067.6 mean_of_5
  3 65212.0 mean_of_5
  4 83000.0 mean_of_5
  5 84520.8 mean_of_5
  6 54170.0 mean_of_5
  > 
  > # 20개의 값의 평균으로 이뤄진 표본을 하나 생성한다
  > samp_data_20 <- data.frame(
  +               income = tapply(sample(loans_income, 1000*20),
  +                            rep(1:1000, rep(20,1000)), FUN=mean),type='mean_of_20')
  > 
  > head(samp_data_20)
      income       type
  1 75542.60 mean_of_20
  2 75513.75 mean_of_20
  3 67449.70 mean_of_20
  4 59384.90 mean_of_20
  5 71645.00 mean_of_20
  6 63369.10 mean_of_20
  > 
  > # 데이터를 하나의 테이블로 생성
  > income <- rbind(samp_data, samp_data_5, samp_data_20)
  > 
  > income$type = factor(income$type,
  +                      levels = c('data_list', 'mean_of_5', 'mean_of_20'),
  +                       labels = c('Data', 'Mean of 5', 'Mean of 20'))
  > # 히스토그램 차트출력
  > ggplot(income, aes(x=income)) +
  +   geom_histogram(bins=40) +
  +   facet_grid(type ~ .)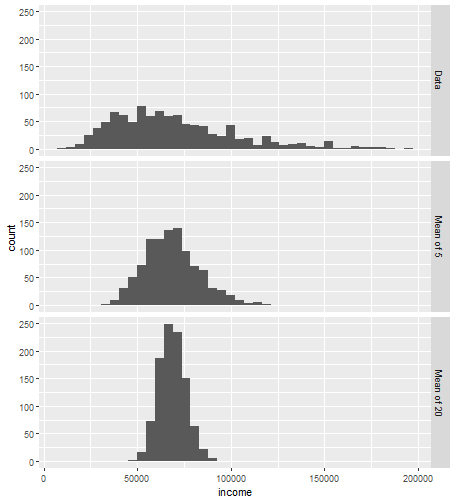
  

  

2.3.1 중심극한정리

• 위와 같이 종모양을 띄는 현상을 중심극한정리라고 한다.
• 표본의 크기가 충분하고 데이터가 정규성을 크게 이탈하지 않는 경우, 여러 표본에서 추출한 평균은 종 모양의 정규 곡선을 따른다.
• 데이터 과학의 관점에서는 부트스트랩을 이용하면 되기 때문에 중심극한정리가 그렇게 중요하지 않다.

2.3.2 표준오차

• 표준오차 : 통계에 대한 표본분포의 변동성을 한미디로 말해주는 단일 측정 지표.
  • cf > 표준편차 : 개별 데이터 포인트의 변동성을 측정.
• 표준오차와 표본크기 사이의 관계를 n제곱근의 법칙이라고 한다.
  • 표준오차를 2배로 줄이려면 표본 크기를 4배로 증가시켜야한다.

2.4 부트스트랩

• 부트스트랩(Bootstrap) : 현재 있는 표본에서 추가적으로 표본을 복원추출하고 각 표본에 대한 통계량과 모델을 다시 계산하는 것.

• 데이터나 표본통계량이 정규분포를 따라야한다는 가정이 꼭 필요하지는 않다.

• 개념적으로는 원래 표본을 수천, 수백만 번 복제하는 것. 이과정을 통해 가상 모집단을 얻게 됨

• 복원추출 바탕임.

• R패키지의 boot를 사용

  stat_fun <- function(x, idx) median(x[idx])
  boot_obj <- boot(loans_income, R = 1000, statistic=stat_fun)
  head(boot_obj)
  

• 부트스트랩은 다변량 데이터에도 적용될 수 있음.

  • 분류 및 회귀 트리(의사결정트리)를 사용할 때, 여러 부트스틒랩 샘플을 가지고 예측값의 평균을 낸다. 이 프로세스를 배깅이라 부른다.

2.4.1 재표본추출 대 부트스트래핑

• 재표본추출 : 여러 표본이 결합되어 비복원추출을 수행할 수 있는 순열 과정을 포함한다.
  • cf ) 부트스트랩은 항상 관측된 데이터로부터 복원 추출함.

---

참고 : 해당 포스트의 내용은 O’REILLY 시리즈 데이터 과학을 위한 통계 ( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.