[DataScience][Study] 데이터 과학을 위한 통계 2-2

---

Chapter 2 데이터와 표본 분포

2.5 신뢰구간

• 신뢰구간 : 오차범위를 이해하기 위한 방법
• 신뢰구간은 항상 90% 또는 95%와 같이 (높은) 백분률로 표현되는 포함 수준과 함께 나옴.
• 대부분의 통계량 혹은 모델 파라미터에 대한 신뢰구간을 생성하는데 부트스트랩을 사용한다.
  • cf > 예전에는 t분포를 사용했다.
• 신뢰수준 : 같은 모집단으로부터 같은 방식으로 얻은 관심 통게량을 포함할 것으로 예상되는, 신뢰구간의 백분율
• 신뢰수준이 높을수록 구간이 더 넓어진다.
• 표본이 작을수록 구간이 넓어진다. (즉, 불확실성이 커진다.)

2.6 정규분포

• 종모양의 정규분포!
• 표본통계량 분포가 보통 어떤 일정한 모양이 있다는 사실은 이 분포를 근사화하는 수학 공식을 개발하는데 강력한 도구가 됨.

2.6.1 표본정규분포와 QQ그림

• x축의 단위가 표준편차로 표현되는 정규분포를 말한다.

• 정규화, 표준화 : 데이터를 표준정규분포와 비교하려면 데이터에서 평균을 뺀 다음 표준편차로 나누면 된다.

• QQ 그림 : 표본이 정규분포에 얼마나 가까운지를 시각적으로 판별하는데 사용된다.

• R의 qqnorm 함수를 사용

  # 정규 분포로부터 추출한 100개 표본의 QQ 그림
  norm_soap <-rnorm(100)
  qqnorm(norm_soap)
  abline(a=0, b=1, col='grey')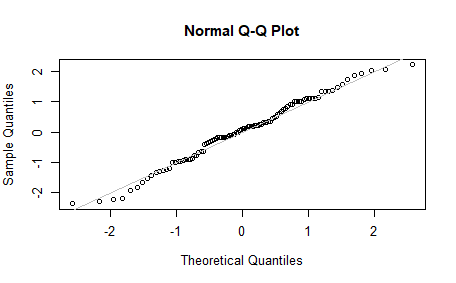
  

  

2.7 긴 꼬리 분포

• 데이터는 일반적으로 정규분포를 따르지 않는다.

• 꼬리 : 적은 수의 극단값이 주로 존재하는, 도수 분포의 길고 좁은 부분

• 왜도 : 분포의 한쪽 꼬리가 반대쪽 다른 꼬리보다 긴 정도

• 주가 수익률 사례

  넷플릭스 의 일일 주식 수익율 QQ그림

  qqnorm(nflx)
  abline(a=0, b=1, col='grey')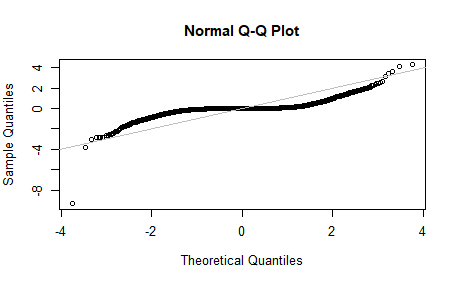
  

  

2.8 스튜던트의 t 분포

• t분포는 정규분포와 생김새가 비슷하지만, 꼬리 부분이 약간 더 두껍고 길다.
• 이것은 표본통계량의 분포를 설명하는 데 광범위하게 사용됨.
• 표본이 클수록 더 정규분포를 닮은 t분포가 형성된다.
• 자유도 : 다른 표본크기, 통계량, 그룹의 수에 따라 t분포를 조절하는 변수
• 표본평균, 두 표본평균 간의 차이, 회귀 파라미터, 그 외 다른 통게량들의 분포를 구할 때 t 분포를 사용
• t분포의 정확도는 표본에 대한 통계량이 분포가 정규분포를 따른다는 조건을 필요로 함.

2.9 이항분포

• 예또는 아니오로 구성됨

• 각 시행은 정해진 확률로 두 가지 결과를 갖는다.

• 통계에서 통상적으로 1이 성공을 의미

• 사례

  • 한 번의 클릭이 판매로 이어질 확률이 0.02일때, 200회 클릭으로 0회 매출을 관찰할 확률은 얼마인가?

• R함수 dbinom으로 이항확률 계산

  > dbinom(2, 5, 0.1)
  [1] 0.0729
  

  5번의 시행에서 0.1의 성공할 확률로 2번 성공할이 나올 확률이다

2.10 푸아송 분포와 그외 관련 분포들

2.10.1 푸아송 분포

• 푸아송 분포(Poisson distribution) : 표집된 단위 시간 혹은 단위 공간에서 발생한 사건의 도수 분포

• 사례 : 5초 동안 서버에 도착한 인터넷 트래픽을 95%의 확률로 완벽하게 처리하는 데 필요한 용량은 얼마 일까?

• 핵심 파라미터는 람다 λ : 어떤 일정 시간/공간 구간 안에서 발생한 평균 사건 수를 의미한다.

• R에서는 rpois 푸하송 분포를 따르는 난수를 생성한다.

  > rpois(100, lambda = 2)
    [1] 4 1 5 2 1 1 3 1 2 2 5 1 3 5 0 3 1 4 3 2 4 0 2 3 3 4 3 1 1 5 2 3 2 3 1
   [36] 1 3 2 1 2 0 2 1 3 1 1 3 4 3 2 4 2 3 2 1 2 5 0 3 2 5 1 2 0 2 1 3 1 4 3
   [71] 1 3 4 2 0 3 2 2 4 0 2 3 0 0 1 3 3 1 1 1 1 0 3 5 4 2 0 2 6 0
  

  람다가 2인 푸아송 분포에서 100개의 난수를 생성한다. 예를 들어 고객 서비스 센터에 접수되는 문의 전화가 분당 평균 2회면, 이 코드는 100분을 시뮬레이션하여 100분당 문의 전화 횟수를 알려준다.

2.10.2 지수분포

• 푸아송 분포에 사용된 것과 동일한 변수 λ 를 사용하여 사건과 사건간의 시간 분포를 모델링 할 수 있다.

• 지수분포에서 난수를 생성하기 위한 R코드에는 두개의 인수(n:난수발생개수, 비율:시간 주기당 사건 수)를 사용한다.

  > rexp(100, .2)
    [1]  4.89032789  1.87917701  0.94369015  1.09388834  2.63866824
    [6] 19.58169567  0.78232587  3.76376749 10.24511988  0.55659505
   [11]  0.39295529  0.65386674  1.42255984  1.02629568  0.06980001
   [16]  8.72246453 10.38048918  6.00721315  1.52330876  2.54315423
   [21]  6.72313007 14.69038993 10.40341812 19.97185911  2.29483266
   [26]  8.95874154  8.83708051  1.07400204  1.90089178  3.23100773
   [31]  8.09904698  1.30160461  7.08739293  0.20219003  0.13756829
   [36]  2.22625187 13.75340036  6.01822799  2.32967261  0.33881706
   [41]  3.98718834  6.36402466  4.84307572 16.33209519  4.30387981
   [46]  7.97386502  4.21362625  0.71189571 12.46156706  3.07522182
   [51] 19.65211066 10.98416314  2.21297609  0.18113880  0.42490512
   [56]  6.62312459 16.01672176  0.35786323  2.28203726  4.41303488
   [61]  9.79308614 14.29675754  3.66913180  2.68006384  3.66116706
   [66]  0.10484349  4.37495109  4.01470877  4.74967368  2.20442073
   [71]  8.39384080  3.73869946  3.87860378  4.00422333  0.76833609
   [76] 10.07228537  1.33561938  8.54823727  2.55801686  0.36906138
   [81]  1.00442282  6.72958904  2.02592069 19.54814404  3.43403516
   [86]  6.03862713  5.00998874 10.51375299  1.30578490  2.31379064
   [91]  8.94005354  0.82902667  7.28256563  2.43419438  2.32160818
   [96]  0.61058312  0.01745534  7.18827899  0.60637946  0.18115840
    
  

2.10.3 고장률 추정

• 데이터가 있긴 하지만 정확하고 신뢰할 만한 발생률을 추정하기에 충분하지 않는 경우, 적합도 검정을 통해 적용한 여러 발생률 중 어떤 것이 관찰된 데이터에 가장 적합한지를 알 수 있다.

2.10.4 베이불 분포

• 사건 발생률이 시간에 따라 지속적으로 변한다면 지수(또는 푸아송) 분포는 더 이상 유용하지 않는다. (ex : 기계 고장)

• 베이불 분포는 지수 분포를 확장한 것.

• 사건 발생률 대신 고장 시간 분석에 사용되기 때문에 두번째 인수는 구간당 사건 발생률 보다는 특성 수명으로 표현.

• R코드는 n(발생개수), shape, scale 세 가지 인수를 사용

  > rweibull(100, 1.5, 5000)
    [1]  5380.9375  6691.5378  4100.5920  7953.0679  3889.7130  4173.8889
    [7]  2685.5007  9070.6176  6292.4638  3748.8321  5185.8654 13434.8004
   [13]  5875.3383  2859.0287  7456.8033  2632.6864  8066.6139  3776.0639
   [19]  6531.9311  1600.6026  7780.2643  2552.9004 10165.3399  5025.5524
   [25]  8765.9956   743.0823  8830.7334  5841.6207   354.7894  1802.6844
   [31]  1586.0677  4166.1805  9365.2644  5605.8606  1642.7748  3324.8302
   [37]  1935.8007  6906.8296  2602.8065  4492.9715 17026.7931  6290.4010
   [43]  4347.6132  4827.1994  8596.1447   154.4313  1266.5012  3611.7161
   [49]  2609.2598 12155.4899  5988.9545  4279.1365  4210.6745  3978.4172
   [55]  6291.0254  2636.0196  2274.7249  7090.6585  6258.7832  2448.6544
   [61]  5149.3144  4226.3066  3368.4101  5317.9316  4584.5655  4640.4981
   [67]  3441.0506  3516.0076   387.5713   640.9331  4579.8923 12625.6605
   [73]  5847.9564  2893.1285  1247.1149  8263.3729  7419.2428  4189.7122
   [79]  6225.2924  2228.6833  1097.1084  5966.5287  7048.7718  3730.5308
   [85]  3310.0016 10096.3100 10112.0428  1364.3119  4554.1475  7725.6247
   [91]  2236.6044  6697.1230  1852.0826  4623.1949  1504.1300  5991.0549
   [97]  4751.0422  8704.9574  1708.8692  6843.0442
    
  

  1.5의 형상 파라미터와 5,000의 특성 수명을 갖는 베이불 분포에서 100개의 난수(수명)을 생성한다.

---

참고 : 해당 포스트의 내용은 O’REILLY 시리즈 데이터 과학을 위한 통계 ( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.