[DataScience][Study] 데이터 과학을 위한 통계 3-1

5 분 소요

Chapter 3. 통계적 실험과 유의성 검정 (1)

실험설계
- 통계 분석의 토대
- 어떤 가설을 확인하거나 기각하기 위한 목표를 가짐
전형적인 통계적 추론이라는 파이프 라인속에 있음.
- 가설을 세운다. -> 실험을 설계 한다.-> 데이터를 수집한다. -> 추론과 결과를 도출한다.

3.1 A/B 검정

A/B 검정은 실험군을 두 그룹으로 나누어 어느 쪽이 다른 쪽보다 더 우월한지 입증 하는 실험
두가지 처리법 중 하나는 기준이 되는 기존 방법이나 아무런 처리도 하지 않는다. 이를 대조군이라 함
주로 웹디자인이나 마케팅에 사용
이 실험의 핵심은 피험자가 어떤 특정 처리에 노출되는 것
측정 지표가 연속형변수, 횟수를 나타내는 변수에 따라 결과가 다르게 표시될 수 있음.

3.1.1 대조군은 왜 필요할까?

대조군이 없다면 다른 것들은 동일하다는 보장이 없다.
대상은 일반적으로 웹 방문자이며, 측정하고자 하는 결과는 클릭 수, 구매 수, 방문 기간, 방문한 페이지 수, 특정 페이지 방문여부 등
A/B 검정 실험에서는 미리 하나의 측정지표를 결정해야 함.

3.1.2 왜 하필 A/B 일까? C, D, .. 가 아니라?

데이터 과학자는 가능한 여러 가격 중에서 가장 좋은 가격은 얼마일까?에 관심
- cf ) 전통적인 의미의 통계적 실험에서는 가격 A와 가격 B의 차이가 통계적으로 유의한가? 에 관심
이러한 실험은 멀티암드 밴딧과 같은 유형의 실험설계가 필요함.

3.2 가설 검정

가설 검정, 유의성 검정은 전통적인 통계분석 방법.
목적 : 관찰된 효과가 우연에 의한 것인지 여부를 알아냄.
통계적 가설 검정은 연구자가 랜덤하게 우연히 일어난 일에 속지 않도록 보호하기 위한 방법

3.2.1 귀무가설

실제로 우연히 일어난 일이지만 흔하지 않다.
그룹간의 차이는 우연에 의한 결과 이다. 즉, 원래는 차이가 없다.
귀무가설이 틀렸다는 것을 증명함.

3.2.2 대립가설

가설 검정은 그 성격상 귀무가설 뿐 아니라 그와 대립하는 가설을 포함
귀무 가설과 대립가설은 모든 가성에 대해 설명
- 예시 ) 귀무가설 : A ≤ B / 대립가설 : A > B

3.2.3 일월/이원 가설 검정

A/B 검정은 새로운 방법(기준)이 입증되지 않는 이상 기본 옵션을 계속 사용함.
방향성의 개념이 들어가면 일원(또는 한쪽꼬리) 가설 검정을 사용
- 즉, 우연에 의한 극단적인 결과에 대해 한 방향만을 고려하여 p 값을 계산한다는 의미.
어느쪽으로 속지 않도록 가설검정을 원한다면 이원(또는 양쪽꼬리) 가설을 사용
R을 포함한 여러 소프트웨어에서 양쪽 꼬리 검정 결과를 기본적으로 제공
p 값의 정확성이 그리 중요하지 않은 데이터 과학에서는 그렇게 중요하지 않음.

3.3 재표본추출

재표본 추출
- 목표 : 랜덤한 변동성을 알아보자
- 의미
  - 관찰된 데이터의 값에서 표본을 반복적으로 추출하는 것
  - 또한, 일부 머신러닝 모델의 정확성을 평가하고 향상시키는데에도 적용
  - 부트스트램 데이터 집합을 기반으로 하는 각각의 의사 결정 트리 모델로 부터 나온 예측들로 부터 배깅이라는 절차를 통해 평균 예측값을 구할수 있다.
- 유형
  - 부트스트랩 : 추정의 신뢰성 평가
  - 순열 검증 : 두개 이상의 그룹과 관련된 가설을 검증

3.3.1 순열 검정

두개 이상의 표본이 관여됨
- 통상적으로 A/B 또는 기타 가설검정을 위해 사용되는 그룹들
순열 절차
1. 여러 그룹의 결과를 단일 데이터 집합으로 결합
2. 결합된 데이터를 잘 섞은 후, 그룹 A와 동일한 크기의 표본을 무작위로 (비복원) 추출함.
3. 나머지 데이터에서 그룹 B와 동일한 크기의 샘플을 무작위로 (비복원) 추출
4. C,D 등의 그룹 등에서도 동일한 작업 수행
5. 원래 샘플의 통계량(또는 추정치)과 지금 추출한 재표본에 대한 다시 계산하고 기록.
6. 1~5단계 R 번 반복하여 검정통계량의 순열 분포를 얻음
그룹간의 차이점을 관찰
- 관찰된 차이가 순열로 보이는 차이의 집합에 들어가 있다면 우연히 일어날수 있는 범위 안에 있는 것
- 관찰된 차이가 순열 밖에 있다면, 통계적으로 유의미하다.(우연히 일어날 수 없다.)

3.3.2 예제: 웹 점착성

고가의 서비스를 제공하는 한 회사의 웹디자인 선정 과정
판매가 자주 있지 않고, 판매주기가 길다.
매출 데이터를 얻는데 오랜 시간이 걸리기 때문에, 내부 페이지 이용을 대리 변수로 사용
- 대리 변수 : 참된 관심 변수를 대신하는 변수를 말함.

사람들이 페이지에 머문 시간을 측정.

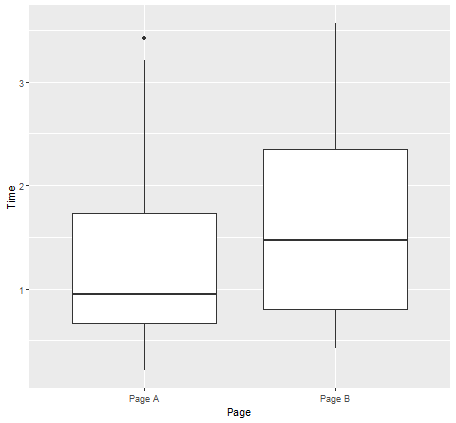
session_times <- read.csv(file = 'source/web_page_data.csv')
library(ggplot2)
ggplot(session_times, aes(x=Page, y = Time)) + geom_boxplot()

페이지 B가 방문객들을 더 오래 붙은 것으로 나타남.

Rplot17

그룹 평균 확인

> mean_a <- mean(session_times[session_times['Page']=='Page A', 'Time'])
> mean_b <- mean(session_times[session_times['Page']=='Page B', 'Time'])
> mean_b-mean_a
[1] 0.3566667

페이지 B는 페이지 A와 비교하여 세션 시간이 평균 0.35초 더 길다.

페이지 A, B의 차이가 우연에 의한 것인지, 통계적으로 유의미한 것인지 판단하기 위해 순열검정을 사용한다.

모든 세션을 결합한 다음, 잘 섞은 후 21개의 그룹(A페이지의 경우 n = 21), 15개의 그룹 (B의 경우 n = 15) 으로 반복하여 추출

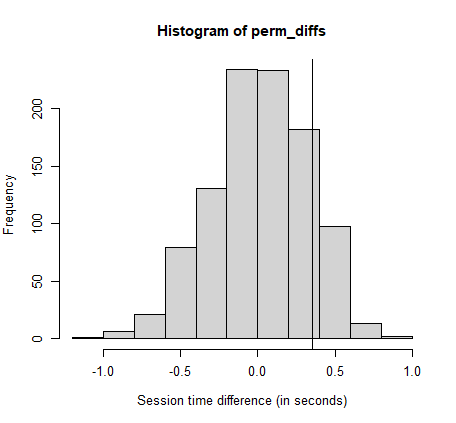
# 비복원 추출 방법으로 n2개의 표본을 추출하여 그룹 B에 할당. 나머지n1개는  A그룹에 할당.
perm_fun <- function (x, n1, n2)
  {
  n <- n1+ n2
  idx_b <- sample(1:n, n1)
  idx_a <- setdiff(1:n, idx_b)
  mean_diff <- mean(x[idx_b]) - mean(x[idx_a])
  return(mean_diff)
}
    
# 위의 함수를 1000번(R=1000) 호출.
perm_diffs <- rep(0,1000)
    
for(i in 1:1000)
  perm_diffs[i] = perm_fun(session_times[, 'Time'], 21, 15)
    
# 히스토 그램 출력
hist(perm_diffs, xlab='Session time difference (in seconds)')
abline(v = mean_b - mean_a)

히스토그램 분석

무작위 순열로 구한 평균 세션 시간의 차이가 가끔 실제 관찰된 시간의 차이(수직선)을 넘어간다.

페이지 A와 B사이의 세션 시간의 차이가 확률분포 내에 있음을 의미

결론적으로, 통계적으로 유의하지 않다.( = 우연이 일어난 것이다.)

Rplot18

3.3.3 전체 및 부트스트랩 순열 검정

앞의 살펴본 랜덤 셔플링 절차를 임의순열검정 또는 임의화검정이라고 부름.
이외 순열검정의 변종
- 전체 순열검정
  - 실제로 나눌수 있는 모든 가능한 조합을 찾음 (무작위로 섞고 나누는 것이 아니라..)
  - 샘플 크기가 비교적 작을때만 실용적
  - 좀 더 정확한 겨론을 보장하는 통계적 속성 때문에 정확이라고도 부름.
- 부트스트랩 순열검정
  - 순열 검정의 비복원 추출 과정을 복원 추출로 진행
  - 모집단에서 개체를 선택할때 뿐만 아니라 개채가 처리 그룹에 할달될때도 임의성 보장.
  - 데이터 과학의 입장에서는 실용적이지 X

3.3.4 순열검정: 데이터 과학의 최종 결론

순열 검정은 휴리스틱한 절차

3.4 통계적 유의성과 p 값

통계적 유의성이랑 결과가 우연히 일어난 것인지, 우연히 일어날 수 없는 극단적인 것인지를 판단하는 방법.
결과가 우연의 변동성 바깥에 존재한다면 통계적으로 유의미하다고 볼 수 있다.
무작위로 순열 추출한 전환율 차이에 대한 히스토그램
```
  
```

3.4.1 p값

p 값 : 통계적 유의성을 정확히 측정하기 위한 지표.
확률모형이 관측된 결과보다 더 극단적인 값을 생성할 빈도
관찰된 차이와 같거다 더 큰 차이를 보이는 경우의 비율로 p값을 추정할 수 있다.
- p 가 0.308이라면 우연히 얻은 결과의 30% 정도가 관찰한 것만큼 극단적이거나 그 이상의 극단적인 결과를 얻은 것으로 기대됨.

R에서는 prop.test 함수 사용

> prop.test(x=c(200,182), n=c(23739,22588), alternative = "greater")
  
  2-sample test for equality of proportions with continuity
	correction
  
data:  c(200, 182) out of c(23739, 22588)
X-squared = 0.14893, df = 1, p-value = 0.3498
alternative hypothesis: greater
95 percent confidence interval:
 -0.001057439  1.000000000
sample estimates:
     prop 1      prop 2 
0.008424955 0.008057376 

x : 각 그룹의 성공 횟수

n : 시행 횟수

정규근사법을 통해, 순열검정에서 얻은 p 값과 비슷한 0.3498을 얻었다.

3.4.2 유의수준

p 값의 의미
- 너무 많은 연구자가 어렴풋이 아는 p 값 개념으로 유의미한 p 값이 나올 때까지 온갖 가설검정을 수행.
- 실제 p 값이 나타내는 것 : 랜덤 모델이 주어졌을 때, 그결과가 관찰된 결과보다 더 극단적일 확률
- 통계적으로 유의미하다는 근거를 가지기엔 약하다.

3.4.3 제1종과 제2종 오류

1종 오류 : 참을 거짓으로 판단
- 보통은 1종 오류를 최소화하도록 가설을 설계한다.
2종 오류 : 거짓을 참으로 판단
- 표본의 크기가 너무 작어서 효과를 알아낼 수 없다고 판단하는 것과 같다.
  
  = 아직 효과가 입증되지 않았다.

3.4.4 데이터 과학과 p 값

p 값은 만능이 아니다.
실험에서 의사결정을 좌우하는 도구로서 사용되선 안된다.
결정에 관련된 정보일 뿐.