[DataScience][Study] 데이터 과학을 위한 통계 4-3
Chapter4. 회귀와 예측
4.6 가정 검정: 회귀 진단
- 모델링과정에서 여러 측정 지표들을 고려하여, 매 단계마다 모델이 데이터에 얼마나 적합한지를 평가함.
- 대부분 모델을 뒷받침하는 가정들을 검정할 수 있는
잔차 분석을 기본으로함 - 예측 설정에 중욯나 통찰을 줄 수 있음
4.6.1 특잇값
-
특잇값 : 대부분의 측정치에서 멀리 벗어난 값을 의미. 극단값.
- 회귀에서는 실제 y값이 예측된 값에서 멀리 떨어져 있는 경우를 말함.
-
표준화 잔차
- 잔차를 표준오차로 나눈 값
- 회귀에서 회귀선으로부터 떨어진 정도를 표준오차 개수로 표현한 값.
-
특잇값과 정상값을 구분하는 통계 이론은 없음
-
특잇값이라고 정하는 것은 다수 데이터로부터 얼마나 떨어져 있어야 하는지에 대한 (임의의)경험칙이 존재.
- 예 : 상자 그림에서 상자 경계선 바깥에 위치한 점들을 특잇값.
-
사례 분석 : 킹카운티 주택 매매데이터의 우편번호가 98105인 지역의 데이터
-
회귀모형 확인
> house_98105 <- house[house$ZipCode == 98105, ] > lm_98105 <- lm(AdjSalePrice ~ SqFtTotLiving+ SqFtLot+ Bathrooms+ + Bedrooms+ BldgGrade, data =house_98105) > lm_98105 Call: lm(formula = AdjSalePrice ~ SqFtTotLiving + SqFtLot + Bathrooms + Bedrooms + BldgGrade, data = house_98105) Coefficients: (Intercept) SqFtTotLiving SqFtLot Bathrooms Bedrooms BldgGrade -772549.86 209.60 38.93 2282.26 -26320.27 130000.10 -
표준화 잔차, 가장 작은 잔차의 위치 구하기
> sresid <- rstandard(lm_98105) > idx <- order(sresid) > sresid[idx[1]] 24333 -4.326732표준 오차의 4배 이상이나 회귀식과의 차이를 보임. 이에 해당하는 추정치는 757,753달러
-
이 특잇값에 해당하는 레코드
> house_98105[idx[1], c('AdjSalePrice' , 'SqFtTotLiving', 'SqFtLot', 'Bathrooms', + 'Bedrooms', 'BldgGrade')] AdjSalePrice SqFtTotLiving SqFtLot Bathrooms Bedrooms BldgGrade 24333 119748 2900 7276 3 6 7이 우편번호에 해당하는 지역에서 이정도 평수 라면 119,748달러보다는 더 비싸야 정상임.
이런 경우는 비정상적인 판매로 회귀에 포함해서는 안됨.
-
- 새로운 데이터를 예측하기 위한 회귀분석에서 특잇값은 중요하지 않을수도 있음
- 하지만 특잇값 검출이 주목적이라면 중요해짐.
4.6.2 영향값
-
주영향관측값(influential observation) : 회귀모형에서 제외됐을 때 모델에 중요한 변화를 가져오는 값
- 회귀분석에서 잔차가 크다고해서 모두 이런값이 되는 것은 아님.
-
단일 레코드의 영향력을 결정하는 지표
-
햇값(hat-value) : 레버리지를 측정하는 일반적인 척도
- 2(P+1)/n 이상의 값들은 레버리지가 높은 데이터 값을 나타냄
-
쿡의거리(Cook’s distance) : 레버리지와 잔차의 크기를 합쳐서 영향력을 판단
- 경험칙에 따르면 쿡의 거리가 4/(n-P-1)보다 크면 영향력이 높다고 보는
-
-
영향력그림, 거품그림 R차트 : 표준화잔차, 햇 값, 쿡의거리를 모두 한그림에 표현
std_resid <- rstandard(lm_98105) cooks_D <- cooks.distance(lm_98105) hat_values <- hatvalues(lm_98105) # cex 옵션 : cooks_D 크기만큼 원으로 표현 # x 축 햇값, y 축 잔차 정보 plot(hat_values, std_resid, cex=10*sqrt(cooks_D)) abline(h=c(-2.5, 2.5), lty=2)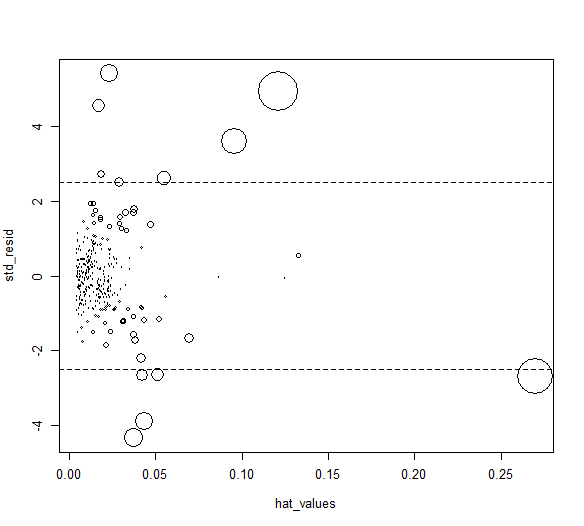
-
회귀모형을 구하는 목적이 새로 들어오는 값에 대해 믿을 만한 예측값을 얻기 위함이라면, 데이터의 크기가 작을 경우에만 영향력이 큰 관측 데이터를 확인하는 작업이 유용
4.6.3 이분산성, 비정규성, 오차 간 상관
-
통계학자들은 잔치에 관심이 많지만 데이터 과학자라면 잔차 분포에 너무 많은 신경을 쓸 필요는 없음.
-
형식적 추론이 완전히 유효할 조건
1) 동일한 분산을 가지며
2) 정규분포를 따르고
3) 서로 독립이라는 가정이 필요
1) 이분산성
다양한 범위의 예측값에 따라 잔차의 분산이 일정하지 않은 것, 즉 어떤 일부분에서의 오차가 다른 데보다 훨씬 크게 나타나는 것
- R의 ggplot2 패키지 이용하여 절대 잔차와 예측값의 관계 도식화
> df <- data.frame(
+ resid = residuals(lm_98105),
+ pred = predict(lm_98105))
>
> head(df)
resid pred
1036 -456062.23 1282201.2
1769 -158145.20 831400.2
1770 -62978.33 718856.3
1771 -186794.02 830548.0
1783 -99686.53 1445665.5
1784 -132968.39 927540.4
>
> library(ggplot2)
>
> ggplot(df, aes(pred, abs(resid))) +
+ geom_point() +
+ geom_smooth()
`geom_smooth()` using method = 'loess' and formula 'y ~ x'
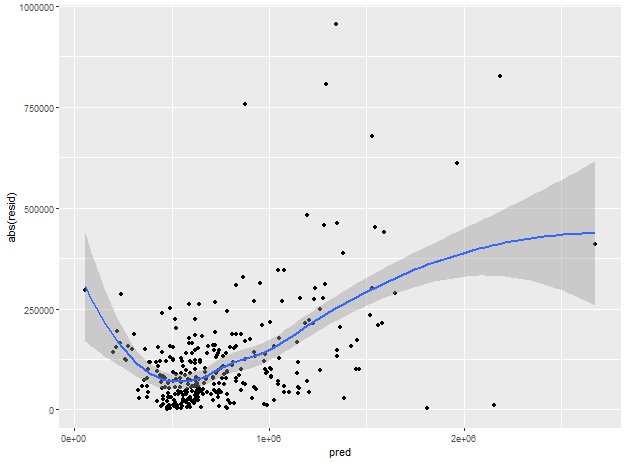
잔차의 분산은 고가의 주택일수록 증가하는 경향이 있음
가격이 낮은 주택의 경우에도 마찬가지로 큰 편
이를 통해 lm_98105는 이분산성 오차를 갖고 있다고 볼 수 있음
2) 비정규성
- lm_98105 회귀모형에서 표준화잔차에 대한 히스토그램에서도 정규분포보다 확연히 더 긴꼬리를 나타냄.
3) 오차간 상관
- 통계학자들은 오차가 독립적이라는 가정을 점검하기도 함.
- 시간에 따른 데이터를 수집하는 경우 특히 그렇다.
- 더빈-왓슷 통계량 (Durbin-Watson statics) : 시계열 데이터를 다루는 회귀분석에서 유의미한 자기상관이 있는지를 탐지하는데 사용
4.6.4 편잔차그림과 비선형성
-
편잔차그림
- 예측 모델이 예측변수와 결과변수 간의 관계를 얼마나 잘 설명하는지 시각화 하는 방법
- 하나의 예측변수와 응답변수 사이의 관계를 모든 다른 예측변수로부터 분리하는 것.
- 편잔차 : 단일 예측변수를 기반으로 한 예측값과 전체를 고려한 회귀식의 실제 잔차를 결합하여
만든 결과
-
R의 predict 함수를 이용해서 개별회귀 항를 구할 수 있다.
> terms <- predict(lm_98105, type = 'terms') > partial_resid <- resid(lm_98105) + terms > partial_resid SqFtTotLiving SqFtLot Bathrooms Bedrooms BldgGrade 1036 -9582.44883 -357174.9708 -450660.995 -524932.2009 -412036.63955 1769 -189558.76910 -78529.9327 -159020.193 -174374.6343 -114119.61053 1770 -98583.94036 11964.9452 -63853.317 -52887.4899 -148952.83461 1771 -130174.59786 -92384.0872 -187669.007 -176703.1797 -272768.52442 1783 306968.80331 48451.3706 -96567.562 -142236.2342 74339.15810 ..................... -
편잔차 분포 위에 평활 곡선
> df <- data.frame(SqFtTotLiving = house_98105[, 'SqFtTotLiving'], + Terms = terms[, 'SqFtTotLiving'], + PartialResid = partial_resid[, 'SqFtTotLiving']) > head(df) SqFtTotLiving Terms PartialResid 1036 4200 446479.78 -9582.449 1769 1920 -31413.57 -189558.769 1770 1900 -35605.61 -98583.940 1771 2340 56619.42 -130174.598 1783 4010 406655.34 306968.803 1784 2570 104827.96 -28140.435 > ggplot(df, aes(SqFtTotLiving,PartialResid )) + + geom_point(shape =1) + scale_shape(solid=FALSE) + + geom_smooth(linetype=2) + + geom_line(aes(SqFtTotLiving, Terms)) `geom_smooth()` using method = 'loess' and formula 'y ~ x'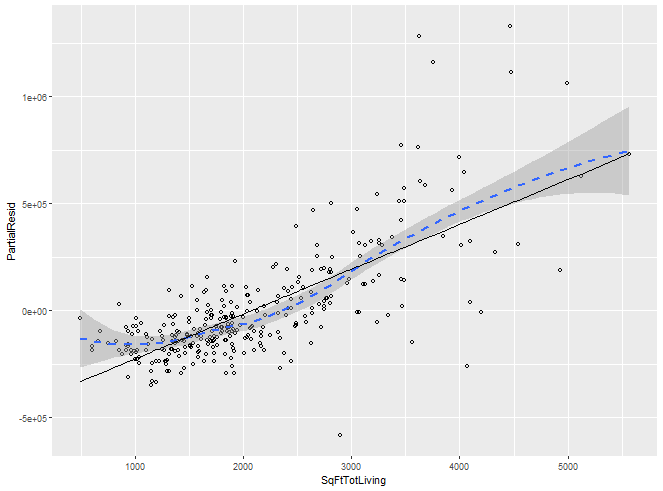
- 편잔차는 SqFtTotLiving 변수가 주택 가격에 얼마나 영향을 미치지는 보여줌
- SqFtTotLiving 변수와 가격 사이의 관계는 분명히 비선형
- SqFtTotLiving에대해 단순선형 항 대신 비선형 항을 고려할 것을 생각해볼 수 있다.
4.7 다항회귀와 스플라인 회귀
- 응답변수와 예측변수 간의 관계가 반드시 선형일 필요 X
- 약물 복용량에 따른 반응은 일반적으로 비선형을 띈다.(복욕량을 두 배로 늘린다고 두 배의 반응이 나타나는 것 아님.)
- 비선형 효과를 회귀분석에 담기 위한 회귀모형을 확장하는 몇가지 방법
- 다향회귀, 스플라인 회귀, 일반화가법모형
4.7.1 다항식
-
회귀식에 다항 항을 포함한 것을 말함
-
R의 ploy 함수를 이용해 구할 수 있다.
킹 주택 데이터로 구한
SqFtTotLiving에 대해 이차 다항식을 피팅하는 과정> lm(AdjSalePrice ~ poly(SqFtTotLiving, 2)+ SqFtLot+ Bathrooms+ + Bedrooms+ BldgGrade, data =house_98105) Call: lm(formula = AdjSalePrice ~ poly(SqFtTotLiving, 2) + SqFtLot + Bathrooms + Bedrooms + BldgGrade, data = house_98105) Coefficients: (Intercept) poly(SqFtTotLiving, 2)1 poly(SqFtTotLiving, 2)2 -402530.47 3271519.49 776934.02 SqFtLot Bathrooms Bedrooms 32.56 -1435.12 -9191.94 BldgGrade 135717.06SqFtTotLiving에 대한 두 가지 계수가 존재(선형항 , 이차 항)
4.7.2 스플라인
-
다항회귀는 비선형 관계에 대해 어느 정도의 곡률을 담아낼 수 있지만, 3, 4, N차 다항식에는 바람직하지 않음.
-
스플라인 : 고정된 점들 사이를 부드럽게 보간하는 방법, 조각별 연속 다항식
-
구간별 다항식은 예측변수를 위한 일련의 고정된 점(매듭) 사이를 부드럽게 연결
-
R패키지 splines를 사용하여 회귀모형에서 b-스플라인 항을 생성.
> library(splines) > knots <- quantile(house_98105$SqFtTotLiving, p = c(.25, .5, .75)) > lm(AdjSalePrice ~ bs(SqFtTotLiving, knots = knots, degree=3)+ SqFtLot+ Bathrooms+ + Bedrooms+ BldgGrade, data =house_98105) Call: lm(formula = AdjSalePrice ~ bs(SqFtTotLiving, knots = knots, degree = 3) + SqFtLot + Bathrooms + Bedrooms + BldgGrade, data = house_98105) Coefficients: (Intercept) -414157.61 bs(SqFtTotLiving, knots = knots, degree = 3)1 -199529.76 bs(SqFtTotLiving, knots = knots, degree = 3)2 -120580.64 bs(SqFtTotLiving, knots = knots, degree = 3)3 -71644.39 bs(SqFtTotLiving, knots = knots, degree = 3)4 195677.89 bs(SqFtTotLiving, knots = knots, degree = 3)5 845244.25 bs(SqFtTotLiving, knots = knots, degree = 3)6 695545.67 SqFtLot 33.33 Bathrooms -4778.21 Bedrooms -5778.70 BldgGrade 134462.37- 하지만 무조건 스플라인 회귀가 더 좋다는 것은 아님.
- 교란변수 때문에 예측 결과가 맞지 않을 수도 있다.
4.7.3 일반화가법모형
-
일반화가법모형(GAM) : 스플라인 회귀를 자동으로 찾는 기술
-
R의 gam 패키지로 주택 데이터 GAM 모델을 피팅
library(mgcv) lm_gam <- gam(AdjSalePrice ~ s(SqFtTotLiving)+ SqFtLot+ Bathrooms+ Bedrooms+ BldgGrade, data =house_98105)s(SqFtTotLiving) 라는 옵션이 스플라인 항에 대한
최적매듭 점을 찾도록 gam 함수에 지시함.
참고 : 해당 포스트의 내용은 O’REILLY 시리즈
데이터 과학을 위한 통계( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.
댓글남기기