[DataScience][Study] 데이터 과학을 위한 통계 5-1
Chapter 5. 분류
- 분류 : 가장 중요한 예측 유형.
- 데이터가 0인지 1인지 (피싱인지/아닌지, 클릭할지/클릭하지 않을지, 변경할지/변경하지 않을지)
- 이진 분류 뿐 아니라, 범주의 개수가 두 가지 이상인 분류를 해야할 필요도 있음.
- 즉,
각 클래스에 속할 예측 확률을 구하는 것이 목적 - 대부분의 알고리즘은 관심 클래스에 속할 확률 점수(경향)를 반환
5.1 나이브 베이즈
- 나이브 베이즈 알고리즘 : 주어진 결과에 대해 예측변수 값을 관찰할 확률을 사용하여, 예측변수가 주어졌을때, 결과 Y = i를 관찰할 확률을 추정한다.
나이브 하지 않은베이지언 분류- 예측 변수 프로파일이 동일한 모든 레코드들을 찾아 가장 많이 속한 클래스를 정함.
- 이 방법은 모든 예측변수들이 동일하다면 같은 클래스에 할당될 가능성이 높기 때문에, 표본에 새로 들어온 레코드와 정확히 일치하는 데이터를 찾는 것에 무게를 두는 방식이다.
5.1.1 나이브하지 않은 베이지언 분류를 왜 현실성이 없을까?
- 답 : 에측 변수의 개수가 일정정도 커지게 되면, 분류해야 하는 데이터들은 대부분은 서로 완전 일치하는 경우가 거의 없다.
5.1.2 나이브한 해법
- 나이브 베이즈 방법에서는 확률을 계산하기 위해 정확히 일치하는 레코드로만 재현할 필요는 없다.
-
대신 전체 데이터를 활용함.
-
특성들 사이의 독립을 가정하는 베이즈 정리를 적용한 확률 분류기의 일종
-
R의 klaR
# 나이브 베이즈 모델 패키지 불러옴. > library(klaR) > > # 원본 데이터 > loan_data <- read.csv(file = 'source/loan_data.csv') > head(loan_data) X status loan_amnt term annual_inc dti payment_inc_ratio revol_bal 1 1 Charged Off 2500 60 months 30000 1.00 2.39320 1687 2 2 Charged Off 5600 60 months 40000 5.55 4.57170 5210 3 3 Charged Off 5375 60 months 15000 18.08 9.71600 9279 4 4 Charged Off 9000 36 months 30000 10.08 12.21520 10452 5 5 Charged Off 10000 36 months 100000 7.06 3.90888 11997 6 6 Charged Off 21000 36 months 105000 13.22 8.01977 32135 revol_util purpose home_ownership delinq_2yrs_zero pub_rec_zero 1 9.4 car RENT 1 1 2 32.6 small_business OWN 1 1 3 36.5 other RENT 1 1 4 91.7 debt_consolidation RENT 1 1 5 55.5 other RENT 1 1 6 90.3 debt_consolidation RENT 1 1 open_acc grade outcome emp_length purpose_ home_ emp_len_ 1 3 4.8 default 1 major_purchase RENT > 1 Year 2 11 1.4 default 5 small_business OWN > 1 Year 3 2 6.0 default 1 other RENT > 1 Year 4 4 4.2 default 1 debt_consolidation RENT > 1 Year 5 14 5.4 default 4 other RENT > 1 Year 6 7 5.8 default 11 debt_consolidation RENT > 1 Year borrower_score 1 0.65 2 0.80 3 0.60 4 0.50 5 0.55 6 0.40 > # 미리 outcome에 대해서 order 작업 > loan_data$outcome <- ordered(loan_data$outcome, levels=c('paid off', 'default')) > # 나이브 베이즈 적용 > naive_model <- NaiveBayes(outcome ~ purpose + home_ + emp_len_ , + data = na.omit(loan_data)) > # 나이브 베이즈 테이블 출력 > naive_model$tables $purpose var grouping car credit_card debt_consolidation home_improvement paid off 0.020731331 0.187596489 0.552159146 0.063164395 default 0.013629747 0.151515152 0.575713467 0.051916545 var grouping house major_purchase medical moving other paid off 0.008336642 0.032861365 0.014247276 0.009262935 0.070574743 default 0.007895549 0.023642539 0.014335495 0.010850867 0.087556791 var grouping small_business vacation wedding paid off 0.020995986 0.006263508 0.013806184 default 0.045741255 0.006969256 0.010233338 $home_ var grouping MORTGAGE OWN RENT paid off 0.4894800 0.0808963 0.4296237 default 0.4313440 0.0832782 0.4853778 $emp_len_ var grouping < 1 Year > 1 Year paid off 0.03105289 0.96894711 default 0.04728508 0.95271492이 모델은 연체를 예상함.
5.1.3 수치형 예측변수
- 베이지언 분류기는 예측 변수들이 범주형인 경우 적합
- 범주형 : 스팸 메일 분류에서 특정 단어, 어구, 문자열의 존재 여부등..
- 수치형을 적용하기 위해선 아래2가지 방법이 있음
- 수치형 예측변수를 비닝(binnig) 하여
범주형으로 변환뒤, 알고리즘 적용 - 조건부 확률을 추정하기 위한 정규분포 같은 확률모형 사용
- 수치형 예측변수를 비닝(binnig) 하여
5.2 판별분석
- 판별분석 (discriminant anlaysis) : 초창기의 통계 분류 방법
- 종류 : 선형판별분석 (LDA : Linear discriminant analysis)
- 주성분분석과 같이 아직도 많이 사용되는 다른 방법들과도 연결
- 판변분석은 에측 변수들의 중요성을 측정하거나 효과적으로 특징을 선택하는 방법으로 사용
5.2.1 공분산 행렬
- 두 개 이상의 변수 사이에 공분산이라는 개념이 사전 이해 필요
- 공분산 : 두 변수 x와 z 사이의 관계를 의미하는 지표
- 상관게수때와 마찬가지로 양수는 양의관계를, 음수는 음의 관계를 의미함.
- cf 상관계수의 범위
-1에서1, 공분산 x와 z에서 사용하는 척도와 동일한 척도에서 정의
5.2.2 피셔의 선형판별
- 피셔의 선형 판별 : 그룹 아느이 편차와 다른 그룹간의 편차를 구분.
- 사례 : 두 개의 연속형 변수 (x,z)를 사용하여, 이진 결과변수 y를 예측하려는 분류 문제
- 기술적으로 판변분석은 보통 에측변수가 정규분포를 따르는 연속적인 변수라는 가정이 있지만, 실제로는 정규분포에서 벗어나거나 이진 예측변수에 대해서도 잘 동작함.
5.2.3 간단한 예
-
R의 MASS 패키지에서 제공하는 LDA 함수
두 예측변수 borrower_score 와 payment_inc_ratio를 이용해 대출 데이터 표본에 이 함수를 적용하고 선형판별자 가중치를 구함.
> library(MASS) > > loan3000 <- read.csv(file = 'source/loan3000.csv') > loan3000$outcome <- ordered(loan3000$outcome, levels=c('paid off', 'default')) > > loan_lda <- lda(outcome ~ borrower_score + payment_inc_ratio, + data = loan3000) > loan_lda$scaling LD1 borrower_score -7.17583880 payment_inc_ratio 0.09967559 >lda 함수를 이용해 상환과 연체데 대한 확률 계산
> pred <- predict(loan_lda) > head(pred$posterior) paid off default 1 0.4464563 0.5535437 2 0.4410466 0.5589534 3 0.7273038 0.2726962 4 0.4937462 0.5062538 5 0.3900475 0.6099525 6 0.5892594 0.4107406예측 결과에 대한 시각화 (체납에 대한 확률값을 그래프로 시각화)
library(ggplot2) lda_df <- cbind(loan3000, prob_default=pred$posterior[,'default']) x <- seq(from=.33, to=.73, length=100) y <- seq(from=0, to=20, length=100) newdata <- data.frame(borrower_score=x, payment_inc_ratio=y) pred <- predict(loan_lda, newdata=newdata) lda_df0 <- cbind(newdata, outcome=pred$class) ggplot(data=lda_df, aes(x=borrower_score, y=payment_inc_ratio, color=prob_default)) + geom_point(alpha=.6) + scale_color_gradient2(low='white', high='blue') + scale_x_continuous(expand=c(0,0)) + scale_y_continuous(expand=c(0,0), lim=c(0, 20)) + geom_line(data=lda_df0, col='green', size=2, alpha=.8) + theme_bw()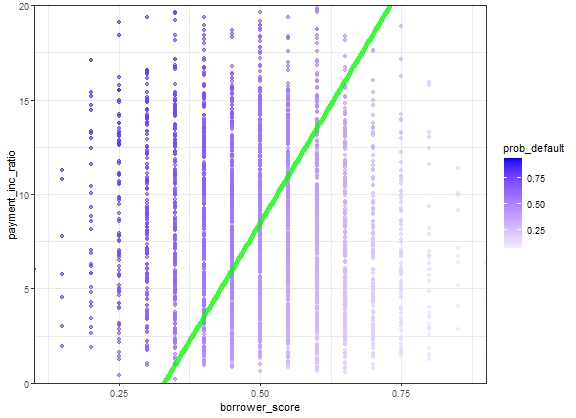
참고 : 해당 포스트의 내용은 O’REILLY 시리즈
데이터 과학을 위한 통계( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.
댓글남기기