[DataScience][Study] 데이터 과학을 위한 통계 5-3

---

Chapter 5. 분류

5.4 분류 모델 평가하기

• 예측 모델링 : 수많은 모델을 시도해보고 각각에 홀드아웃 표본을 적용하고 성능을 평가하는 것은 아주 일반적
  • 홀드아웃 표본 : 시험 표본(test sample) 혹은 타당성 표본(validation sample)
• 용어정리
  • 민감도(sensitivity) : 정확히 분류된 1의 비율 , (유의어 :재현율 recall)
  • 특이도(specificity) : 정확히 분류된 0의 비율
  • 정밀도(precision) : 정확히 1이라고 예측된 1의 비율
  • ROC 곡선 : 민감도와 특이성을 표시한 그림
• 분류 성능 측정 방법 : 정확히 예측한 것들의 비율이 얼마인지 보는 것
  • 대부분 분류 알고리즘에서는 각 데이터에 대해 1이 될 확률값을 추정하여 할당.
  • 기본적인 컷오프 기준값은 0.5, 즉 50%
    • 확률이 0.5보다 크면 분류 결과는 1, 그렇지 않으면 0

5.4.1 혼동행렬

• 혼동행렬

  • 분류 결과를 나타내는 가장 대표적인 행렬

  • 응답 유형별로 정확한 예측과 잘못된 예측의 수를 한 번에 보여주는 표

  • 사례 적용 : 동일한 수의 대출 연체/상환 데이터를 이용해 학습한 모델

    • Y=1은 관심있는 사건 (연체)
    • Y=0은 그 반대인 통상적인 사전(상환)
    • 전체 훈련 데이터(불균형)에 적용한 logistic_gam 모델의 혼동 행렬 계산 ```R pred <- predict(logistic_gam, newdata = loan_data) pred_y <- as.numeric(pred > 0) true_y <- as.numeric(loan_data$outcome == ‘default’) true_pos <- (true_y==1) & (pred_y==1) true_neg <- (true_y==0) & (pred_y==0) false_pos <- (true_y==0) & (pred_y==1) false_neg <- (true_y==1) & (pred_y==0) conf_mat <- matrix(c(sum(true_pos), sum(false_pos),
    • sum(false_neg), sum(true_neg)), 2, 2) colnames(conf_mat) <- c(‘Yhat = 1’, ‘Yhat = 0’) rownames(conf_mat) <- c(‘Y = 1’,’Y = 0’ ) conf_mat Yhat = 1 Yhat = 0 Y = 1 14293 8378 Y = 0 8051 14620 ```

    • 결과에서 열은 예측값이고 행은 실제 결과

    • 예를 들면 14,293건의 연체는 정확히 연체라는 예측 결과를 보였지만, 8,501건의 연체는 대출을 상환한다고 잘못된 예측을 함.

5.4.2 희귀 클래스 문제

• 많은 문제의 경우 한 클래스가 다른 클래스에 비해 경우의 수가 훨씬 많은 경우가 존재
• 1 : 데이터 수가 상대적으로 작은(희귀한) 클래스, 관심의 대상, 더 중요한 사건,
• 0 : 수가 많은 경우, 클래스 분리가 어려운 경우엔 가장 정확도가 높은 분류 모델은 무조건 0으로 분류하는 모델일 수도 있음.

5.4.3 정밀도, 재현율, 특이도

• 정밀도 : 예측된 양성 결과의 정확도

• 재현율(recall), 민감도 : 양성 결과를 예측하는 모델의 능력을 평가

  • 양성 데이터에 대해 정확히 1이라고 예측하는 결과의 비율
  • 민감도 : 생물 통계학과 의료진단학에서 주로 사용
  • 재현율 : 머신러닝 분야에서 좀더 많이 사용

  > #정밀도
  > conf_mat[1,1]/sum(conf_mat[,1])
  [1] 0.6396796
  > #재현율(recall)
  > conf_mat[1,1]/sum(conf_mat[1,])
  [1] 0.630453
  > #특이도(specificity)
  > conf_mat[2,2]/sum(conf_mat[2,])
  [1] 0.6448767
  

5.4.4 ROC 곡선

• 재현율과 특이도 사이에는 트레이드오프 관계(시소관계)

  • 1을 잘 잡아낸다는 것은 그만큼 0과 1을 잘못 예측할 가능성도 높아짐을 의미

• 이상적인 분류기 : 0을 1로 잘못 분류하지 않으면, 동시에 1을 정말 잘 분류하는 분류기

• ROC(reciever operation characteristic)

  • 수신자 조작 특성
  • x축의 특이도에 대한 y축의 재현율(민감도)을 표시

  idx <- order(-pred)
  recall <- cumsum(true_y[idx]==1)/sum(true_y==1)
  specificity <- (sum(true_y==0) - cumsum(true_y[idx]==0)) / sum(true_y==0)
  roc_df <- data.frame(recall = recall, specificity = specificity)
  ggplot(roc_df, aes(x=specificity, y = recall))+
    geom_line(color='blue') +
    scale_x_reverse(expand=c(0,0)) +
    scale_y_continuous(expand = c(0,0))+
    geom_line(data=data.frame(x=(0:100)/100), aes(x=x, y=1-x),
              linetype='dotted', color='red')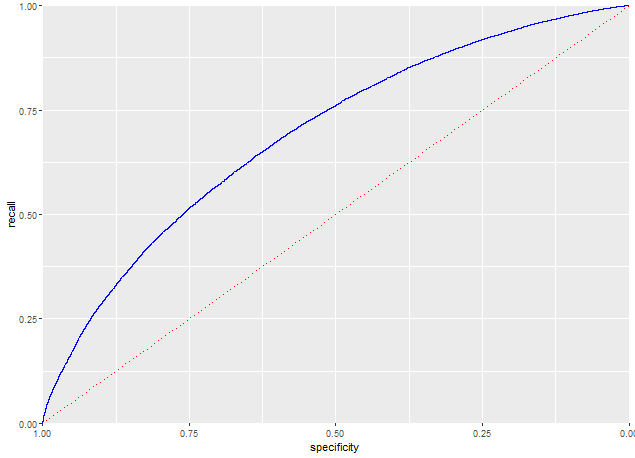
  

  

  • 효과적인 분류기는 ROC 곡선이 왼쪽 상단에 가까운 형태를 보일 것임
    • 즉, 0을 1로 잘못 예측하는 경우 없이, 1을 정확히 예측

5.4.5 AUC

• AUC : ROC 곡선의 아래쪽 면적

  • AUC 값이 높을 수록 더 좋은 분류기
  • AUC 값이 1 이라는 것은 0을 1로 잘못 예측하는 경우 없이, 1을 정확히 분류하는 완벽한 분류기를 의미.
  • 최악의 분류기는 ROC 곡선이 가운데를 지나가는 직석인 경우(즉, AUC가 0.5인경우)

• AUC 수치는 적분을 통해 구할수 있음

  > sum(roc_df$recall[-1] * diff(1-roc_df$specificity))
  [1] 0.6926232
  

  • 모델의 AUC 값은 약 0.69로 상대적으로 약한 분류기

5.4.6 리프트

• 리프트 차트 : 먼저 y 축에 재현율을 그리고 x축에 총 레코드 수를 나타내는 누적이득 차트를 작성해야 함.
• 리프트 곡선 : 랜덤 선택을 의미하는 대각선에 대한 누적이득의 비율
  • 적합한 컷오프 값을 결정하기 위한 중간 단계로 활용할 수 있음.
• 십분위 이득 차트 : 잠재적인 고객을 선별하기 위한 예측 모델

5.5 불균형 데이터 다루기

• 불균형 데이터에서 예측 모델링 성능을 향상시킬 방법

5.5.1 과소표본 추출

• 데이터의 개수가 충분하다면, 다수의 데이터 해당하는 클래스에서 과소표본추출(다운샘플링)을 해서 모델링할 때 0과 1의 데이터 개수를 균형을 맞춤
• 중복된 레코드가 많을것이라는 가정하에 진행
• 소수 클래스의 데이터가 수만개 정도가 충분 (물론 1과 0을 분리하기 쉽다면, 더 적은 데이터로 충분할 수 있음.)

5.5.2 과잉표본추출과 상향/하향 가중치

• 과소표본 방식의 약점 : 일부 데이터가 버려지기 때문에 모든 정보를 활용하지 못함. 유용한 정보까지 버리게 되는 결과를 초래할 수 있음.
• 이럴 경우, 다수 클래스를 과소표본추출하는 대신, 복원추출 방식(부트스트래핑)으로 희귀 클래스의 데이터를 과잉표본추출(업샘플링)해야함.
• 데이터에 가중치를 적용하는 방식도 비슷한 효과를 얻을 수 있음.
• 많은 분류 알고리즘에서 상향/하향 가중치를 데이터에 적요하기 위해 wight라는 인수를 지원

5.5.3 데이터 생성

• 데이터 생성 : 부트스트랩을 통한 업샘플링의 변형으로 기존에 존재하는 데이터를 살짝 바꿔 새로운 레코드를 만드는 방법
• 통계에서 부스팅이나 배깅 같은 앙상블 모델에 담겨 있는 개념과 매우 비슷하다.
• SMOTE(Synthetic Minority Overamploing Technique) 알고리즘가 대표적임.

5.5.4 비용 기반 분류

• 실무적으로 , 분류 규칙을 결정할 때 정확도나 AUC만으롣는 충분하지 않을 수 있음.
• 신규 대출인 경우, 가치가 적은 대출보다는 연체 확률이 더 높더라도 가치가 더 큰 대출을 선호하는 편이 나을 수도 있음.

5.5.5 예측 결과 분석

• AUC와 같은 단일 성능 지표로는 어떤 상황에서 모델의 적합성을 여러 가지 측면에서 보기 어려울 수 도 있음
• 4가지 서로 다른 모델을 적용 후 평가함.
  • 선형판별분석(LDA)
  • 로지스틱 선형회귀
  • GAM을 이용한 로지스틱회귀
  • 트리모델

---

참고 : 해당 포스트의 내용은 O’REILLY 시리즈 데이터 과학을 위한 통계 ( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.