[DataScience][Study] 데이터 과학을 위한 통계 6-1

---

Chapter 6. 통계적 머신러닝

• 통계적 머신러닝 : 회귀나 분류와 같은 예측 모델링을 자동화하기 위한 더 강력한 기술을 개발해 옴.

  • 데이터에 기반

  • 전체적인 구조(ex : 모델이 선형인지)를 가정하지 않는다.

  • 예 : K 최근접 이웃방법

    • 비슷한 레코드들이 어떻게 분류되는지에 따라 해당 레코드를 분류하는 방법
    • 앙상블 학습을 적용한 의사 결정 트리 -> 최고의 성능을 얻을 수 있는 에측 모델링 기법
    • 앙상블의 기본 아이디어는 최종 예측을 얻기 위해 많은 모델을 사용하는 것.
    • 의사 결정 트리는 에측변수와 결과벼수 사이의 관계 규칙을 학습하는 유연하고 자동화된 기술

6.1 K 최근접 이웃

• KNN(K-nearest neighbor) 알고리즘 : 가장 간단한 예측/분류 방법중 하나
  • 특징이 유사한 K의 레코드를 찾아
  • 유사한 레코드들 중에 다수가 속한 클래스가 무엇인지 찾아 분류하고,
  • 유사한 레코드들의 평균을 찾아서 새로운 레코드에 대한 값을 예측한다.
• 모든 예측변수들은 수치형 이어야됨.

6.1.1 예제: 대출 연체 예측

• 개인에게 대출해주는 P2P 방식의 대출업체

• 예측변수 2가지 사용

  • payment_inc_ratio : 소득에 대한 대출 상환 비율
  • dti : 소득에 대한 부채(모기지는 제외) 비율

• K = 20, payment_inc_ratio=9, dti=22.5 일 경우 KNN 예측 결과

  > library(FNN)
    
  > loan200 <- read.csv(file='source/loan200.csv')
  > newloan <- loan200[1, 2:3, drop=FALSE]
  > 
  > knn_pred <- knn(train = loan200[-1, 2:3], test = newloan, cl=loan200[-1,1], k=20)
  > knn_pred == 'paid off'
  [1] TRUE
  

  결과는 새로운 대출은 상환될 것으로 예상됨.

6.1.2 거리 지표

• 유사성(근접성)은 거리지표를 통해 결정
• 거리 지표 : 두 테이터가 서로 얼마나 멀리 떨어져 있는지를 측정하는 함수
  • 유클리드 거리 : 두 벡터 사이에 가장 많이 사용되는 지표, 서로의 차에 대한 제곱합을 구한 뒤 그 값의 제곱근을 취함
  • 맨하탄 거리 : 두 점 사이의 직선 거리, 점과 점 사이의 이동 시간으로 근접성을 다질 때 좋은 지표

6.1.3 원-핫 인코더

• 요인(문자열) 변수는 이진 가변수의 집합으로 변환해야함..
• 하나의 변수 대신에 여러개의 이진 변수로 표현
• 하나의 예측변수를 하나의 1과 여러개의 0으로 이뤄진 벡터 형태로 변환하면 통계적 머신러닝 알고리즘에 사용하기 편리해짐.
• 원-핫 인코딩 : 하나의 비트만 양수(hot)가 허용되는 회로 설정

6.1.4 표준화(정규화, Z 점수)

• 표준화 개념

  • 통계 : 얼마나 평균과 차이가 나는지, 모든 변수에서 평균을 빼고 표준 편차로 나누는 과정을 통해 변수들을 모두 비슷한 값의 범위로 변환
  • 데이터 베이스 : 데이터 베이스 설계시 데이터의 중복을 줄이고 데이터의 의존성을 확인하는 과정

• z 점수 : 평균으로 부터 표준편차만큼 얼마나 떨어져 있는지를 의미함.

• KNN이나 다른 알고리즘(ex : 주성분분석과 클러스터링)에서는 데이터를 미리 표준화 하는것이 필수

• R 에서 표준화 적용

  > loan_df <- model.matrix(~ -1 + payment_inc_ratio + dti + revol_bal +
  +                         revol_util, data=loan_data)
  > 
  > newloan = loan_df[1,, drop=FALSE]
  > loan_df = loan_df[-1,]
  > outcome <- loan_data[-1,1]
  > 
  > knn_pred <- knn(train=loan_df, test=newloan, cl=outcome, k=5)
  > loan_df[attr(knn_pred, "nn.index"),]
        payment_inc_ratio  dti revol_bal revol_util
  35537           1.47212 1.46      1686       10.0
  33652           3.38178 6.37      1688        8.4
  25864           2.36303 1.39      1691        3.5
  42954           1.28160 7.14      1684        3.9
  43600           4.12244 8.98      1684        7.2
  

  • revol_bal 값은 새 데이터 값과 아주 비슷하지만, 다른 예측 변수들은 넓게 퍼져 있는 것을 볼 수있음.
  • 이를 통해 이웃들을 결정할 때 다른 변수들의 역할이 중요하지 않다고 볼수 있다.

• R에서 제공하는 scale 함수

  > loan_std <- scale(loan_df)
  > 
  > knn_pred <- knn(train=loan_std, test=newloan, cl=outcome, k=5)
  > loan_df[attr(knn_pred, "nn.index"),]
        payment_inc_ratio   dti revol_bal revol_util
  43635           3.44454 33.48   1743266       29.5
  5562            2.85093 11.38   1207359       56.0
  5637            2.99452 23.46    508961       91.7
  44393           4.06825 23.61    462076       87.4
  14632           4.84339 16.44    451481       89.9
  

6.1.5 K 선택하기

• K를 선택하는 것은 KNN 성능을 결정하는 중요한 요소
  • K=1 가장 간단한 방법
  • K>1 일때 더 좋은 결과를 보임
• 일반적으로 K가 너무 적으면 오버피팅 문제 발생
• K가 너무 크면 오버스무딩 문제 발생
• 적당한 K를 찾기 위해 홀드아웃 데이터 또는 타당성검사를 위해 따로 떼어놓은 데이터에서의 정확도를 가지고 K 값을 결정하는데 사용함.
• 보통 K는 홀수로 지정한다.

6.1.6 KNN을 통한 피처 엔지니어링

• 다른 분류 방법들의 특정 단계에 사용할 수 있게 모델에 지역적 정보를 추가하기 위해 KNN 사용

  • KNN을 통해 얻은 결과로 피처를 추가함. (원래 예측 변수들을 두번 사용)

• KNN을 통해 얻은 정보는 소수의 근접한 레코드들로부터 얻은 매우 지협적인 정보이기 대문에, 다중공선선 문제를 야기 하지 않는다.

6.2 트리모델

• 트리 모델
  • 회귀 및 분석트리 (classification and regression tree)
  • 의사결정트리 (decision tree)
  • 트리
• 파생된 예측 모델링 기법
  • 랜덤포레스트(Random forest)
  • 부스팅
• if-then-else 규칙 집합체
• 예측변수들 사이의 관계로 단순 트리 모델을 표시할 수 있고, 쉽게 해석

6.2.1 간단한 예제

• R패키지의 rpart, tree 사용

• 3,000개의 대출 데이터에 적합한 트리 모델 구현

  loan_tree <- rpart(outcome ~ borrower_score + payment_inc_ratio,
                     data = loan_data, control = rpart.control(cp=.005))
    
  plot(loan_tree, uniform = TRUE, margin = .05)
  text(loan_tree)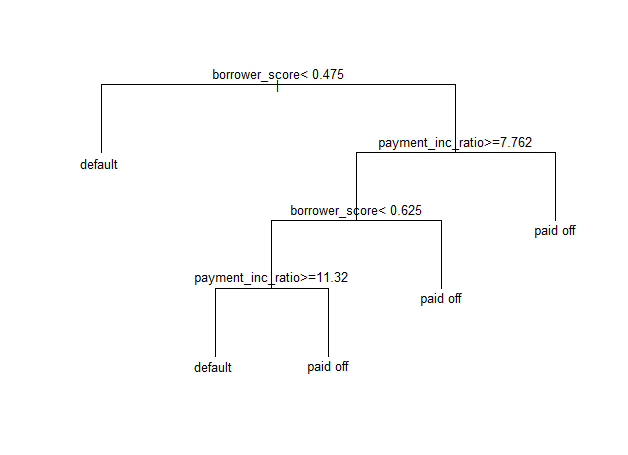
  

  

트리구조 아래 출력

> loan_tree
n= 45342 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 45342 22671 default (0.5000000 0.5000000)  
   2) borrower_score< 0.475 19422  7143 default (0.6322212 0.3677788) *
   3) borrower_score>=0.475 25920 10392 paid off (0.4009259 0.5990741)  
     6) payment_inc_ratio>=7.762325 11528  5619 paid off (0.4874219 0.5125781)  
      12) borrower_score< 0.625 8549  4062 default (0.5248567 0.4751433)  
        24) payment_inc_ratio>=11.31995 4009  1690 default (0.5784485 0.4215515) *
        25) payment_inc_ratio< 11.31995 4540  2168 paid off (0.4775330 0.5224670) *
      13) borrower_score>=0.625 2979  1132 paid off (0.3799933 0.6200067) *
     7) payment_inc_ratio< 7.762325 14392  4773 paid off (0.3316426 0.6683574) *

• 노드 2)에서 7143만큼 오분류(손실)하였음
• 노드 13)에서 62%정도가 대출연체 (대출상환, 대출 연체 비율을 나타냄.)

6.2.2 재귀 분할 알고리즘

• 재귀분할 : 의사 결정 트리를 만들 때 사용하는 알고리즘

• 예측변수 값을 기준으로 데이터를 반복적으로 분할해나감

• 분할할 때에는 상대적으로 같은 클래스의 데이터들끼리 구분되도록 함.

6.2.3 동질성과 불순도 측정하기

• 트리 모델링은 분할 영역 A(기록 집합)를 재귀적으로 만드는 과정
• 트리 모델링 목적 : 분할 영역을 통해 Y=0 혹은 Y=1의 결과를 예측
• 각 분할 영역에 대한 동질성 (혹은 동일한 목적을 위해 불순도를 측정)
• 해당 파티션 내에서 오분류된 레코드의 비율 p로 예측의 정확도 표시 (0 ~ 0.5 사이)
• 불순도 측정 지표
  • 지니 불순도
  • 엔트로피

6.2.4 트리 형성 중지하기

• 트리가 더 커질수록 분할 규칙들은 더 세분화됨
• 과한 세분화는 오버피팅 우려가 있음
• 새로 데이터를 분류할 때 학습 데이터의 노이즈가 생성되어 방해가 됨.
• 이러 방법을 해결하기 위한 방법은 가지치기

• 가지 분할을 멈추는 대표적 방법

  • 분할을 통해 얻어진 하위 영역(잎)의 크기가 너무 작다면 멈춤
  • 새로운 분할 영역이 ‘유의미’하지 않다면, 굳이 분할하지 않음.
• 복잡도 파라미터 (complexity parameter, cp) : rpart에서 트리의 복잡도를 의미
  • cp가 작다면 트리는 실제 의미 있는 신호뿐 아니라 노이즈까지 학습하여 오버피팅 문제 발생
  • cp가 크다면 트리가 너무 작아 예측 능력을 거의 갖지 못함.
  • 최적의 cp를 결정하는 것은 편향-분산 트레이드오프 방법
    • 교차타당성 검사를 통해 에러가 가장적은 값을 cp로 선정

6.2.5 연속값 측정하기

• 트리모델을 통해 연속값을 예측하는 방법(회귀분석)에도 적용할 수 있음
• 회귀분석과 차이점
  • 하위 분할영역에서 평균으로부터의 편차들을 제곱한 값을 이용하여 불순도 측정
  • RMSE(제곱근 평균제곱오차)를 이용해 예측 성능 평가

6.2.6 트리 활용하기

• 장점
  • 트리모델을 데이터 탐색을 위한 시각화 가능(예측변수들 간의 비선형 관계 표현)
  • 일종의 규칙들의 집합 (비전문가와 대화에 효과적)
• 참고
  • 예측에서는 다중 트리에서 나온 결과를 이용하는 것이 효과적
    • 특히 랜덤포레스트나 부스팅 트리 알고리즘은 거의 항상 우수한 예측 정화도나 성능을 보여줌.

---

참고 : 해당 포스트의 내용은 O’REILLY 시리즈 데이터 과학을 위한 통계 ( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.