[DataScience][Study] 데이터 과학을 위한 통계 6-2

7 분 소요

Chapter 6. 통계적 머신러닝

6.3 배깅과 랜덤 포레스트

앙상블 모델 (다중 모델의 평균을 취하는 방식) 은 단일 모델을 사용하는 것보다 더 나은 성능을 보임.
앙상블 모델의 간단한 원리
- 주어진 데이터에 대해 예측모델을 만들고 예측 결과를 기록
- 같은 데이터에 대해 여러 모델을 만들고 결과 기록
- 각 레코드에 대해 예측된 결과들의 평균을 구함.
앙상블 기법은 DT(의사결정트리)에 체계적이고 효과적으로 적용됨.
- 방법 : 배깅, 부스팅
랜덤 포레스트, 부스팅 트리 : 앙상블 기법이 트리 모델에 적용될 경우

6.3.1 배깅

배깅 : 부트스트랩 종합(bootstrap aggregating)의 줄임말
- 배깅은 매번 부트스트랩 재표본에 대해 새로운 모델을 생성
- 다양한 모델들을 정확히 같은 데이터에 대해 구하는 것 X

6.3.2 랜덤 포레스트

개념 : 의사 결정 트리에서 레코드 표본 추출시, 변수 역시 샘플링하는 것이 추가된 배깅 방법
- 기본 트리 알고리즘 + 배깅 + 변수의 부트스트랩 샘플링
알고리즘의 각 단계마다, 고를 수 있는 변수가 랜덤하게 결정된 전체 변수들의 부분집합에 한정.
각 단계 변수 샘플링 갯수 > 보통 전체 변수의 개수가 P일때, 루트 P개 정도 선택함.

R에서 randomForest 패키지

> library(randomForest)
> 
> loan3000 <- read.csv(file = 'source/loan3000.csv')
> loan3000$outcome <- ordered(loan3000$outcome, levels=c('paid off', 'default'))
> rf <- randomForest(outcome ~ borrower_score + payment_inc_ratio,
+                    data = loan3000)
> rf
  
Call:
 randomForest(formula = outcome ~ borrower_score + payment_inc_ratio,      data = loan3000) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 1
  
        OOB estimate of  error rate: 38.27%
Confusion matrix:
         paid off default class.error
paid off      976     579   0.3723473
default       569     876   0.3937716
  

기본적으로 500개의 트리를 학습을 통해 생성

여기서는 예측변수를 두 개만 사용했기 때문에, 둘 중 한 변수를 랜덤하게 선택하게 됨.

즉, 부트스트랩의 크기가 1

OOB(Out of bag) 추정 에러 : 트리 모델을 만들 때 사용했던 학습 데이터에 속하지 않는 데이터를 사용해 구한 학습된 모델의 오차율

모델을 출력해 랜덤포레스트에서 트리의 개수에 따른 OOB 에러 변화 확인

error_df = data.frame(error_rate = rf$err.rate[,'OOB'],
                      num_trees = 1:rf$ntree)
  
ggplot(error_df, aes(x= num_trees, y = error_rate))+
  geom_line()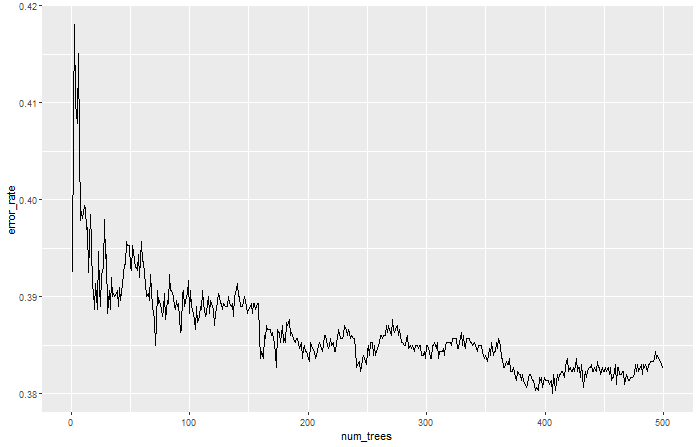

Rplot26

트리가 추가될 때마다 정확도가 개선된다.

predict 함수를 이용해 예측값을 구하고 그래프로 출력

pred <- predict(rf, prob=TRUE)
rf_df <- cbind(loan3000, pred = pred)
ggplot(data=rf_df, aes(x=borrower_score, y = payment_inc_ratio, color=pred,
                       shape=pred))+
  geom_point(alpha=.6, size=2) +
  scale_shape_manual(values=c(46,4))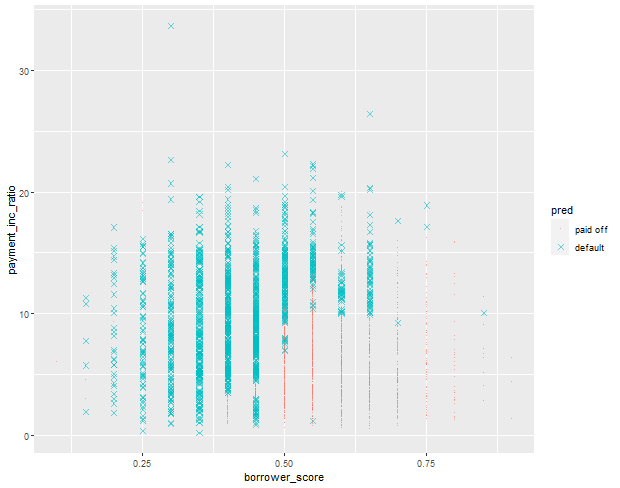

Rplot27

랜던포레스트는 일종의 블랙박스 모델
- 단순 트리보다 정확한 예측 성능
- BUT 직관적인 해석 불가능
예측결과가 일반적이지 않은 예외 사황까지 학습한다면 오버피팅이 발생할 수 있음.

6.3.3 변수 중요도

랜덤 포레스트가 장점이 될 경우
- 피처와 레코드의 개수가 많은 데이터에 대해 예측모델을 만들 때
- 다수의 예측 변수 중 어떤 것이 중요한지, 이들 사이에 존재하는 상관관계 항들에 대응되는 복잡한 관계들을 자동으로 결정함

사례 : 대출 데이터에서 모든 변수를 고려한 모델

> loan_data <- read.csv(file= 'source/loan_data.csv')
>
> # outcome numeric 변수 -> 수치형으로 변경 
> loan_data$outcome = factor(loan_data$outcome)
> rf_all <- randomForest(outcome ~ . , data = loan_data, importance = TRUE)
> rf_all
  
Call:
 randomForest(formula = outcome ~ ., data = loan_data, importance = TRUE) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 4
  
        OOB estimate of  error rate: 0%
Confusion matrix:
         default paid off class.error
default    22671        0           0
paid off       0    22671           0

컴퓨터 사양에 따라 시간이 쫌 걸릴 수 있으므로, 여러번 실행하지 말고 기다려보자!

importance = TRUE : randomForest 함수에 다른 변수들의 중요도에 관한 정보를 추가적으로 저장 요청

varImpPlot 함수 : 변수들의 상대적인 성능을 그래프를 통해 보여줌

varImpPlot(rf_all, type = 1)
varImpPlot(rf_all, type = 2)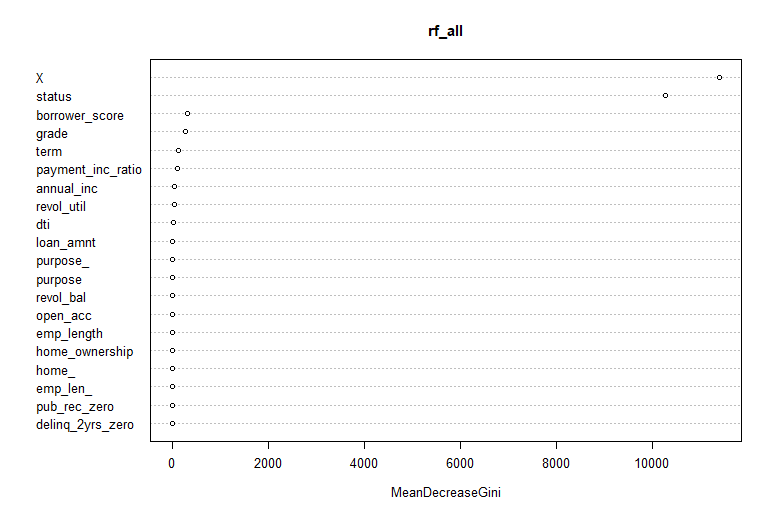

Rplot28

변수 중요도 측정 2가지 방법
- 변수의 값을 랜덤하게 섞었다면, 모델의 정확도가 감소하는 정도를 측정 (type=1)
  - 정확도는 OOB로부터 얻는다(결국, 교차타당성검사와 같은 효과를 가짐.)
- 특정 변수를 기준으로 분할이 일어난 모든 노드에서 불순도 점수의 평균 감소량을 측정(type=2)
  - type=1 에 비해 믿을만 하지 않음.
randomForest 함수는 지니 불순도만 활용 (부차적으로 얻어지는 결과물)
지니 계수 감소와 모델 정확도 감소 사이의 차이를 잘 조사해보면, 변수 중요도를 통해 모델을 개선할 수 있는 아이디어를 얻을 수 있음.

6.3.4 하이퍼파라미터

파라미터(Parameter) vs 하이퍼파라미터(hyperparameter)
- 파라미터(Parameter) : 모델 내부에서 확인 가능한 변수, 데이터를 통해서 산출이 가능한 값.
  - 인공지능 : 가중치, SVM : 서포트 벡터, 선형회귀나 로지스틱회귀분석 : 결정계수
- 하이퍼파라미터(hyperparameter) : 모델 밖에서 확인 가능한 변수, 데이터 분석(알고리즘 구현 과정)을 통해서 얻어지는 값
  - 신경망 학습 : learning rate(학습률), SVM : 코스트값인 C, KNN : K 개수
하이퍼파라미터(hyperparameter) : 랜덤포레스트의 성능을 조절.
오버피팅을 피하기 위해 매우 중요함.
종류
- nodesize : 말단 노드(나무에서 잎 부분)의 크기, 기본은 1, 회귀에서는 5
- maxnodes : 각 DT에서 전체 노드의 최대 개수, 기본적으로는 제한 X, nodesize 제한 설정에 따라 가장 큰 트리의 크기가 결정.
nodesize 와 maxnodes 를 크게 하면 더 작은 트리를 얻게 되고, 거짓 예측 규칙들을 만드는 것을 피할 수 있음.

6.4 부스팅

부스팅 : 앙상블 형태로 만들기 위한 일반적인 방법
- 앙상블 모델 : 예측 모델링 쪽에서 표준 방법이 되고 있음.
결정트리에 많이 사용
훨씬 더 많은 부가 기능을 가짐.
- 이전 모델이 갖는 오차를 줄이는 방향으로 다음 모델을 연속적으로 생성

6.4.1 부스팅 알고리즘

종류
- 에이다 부스트
  - 잔차에 따라 데이터의 가중치를 조절하는 부스팅의 초기 버전
  - 잘못 분류된 관측 데이터에 가중치를 증가 시킴으로써, 현재 성능이 제일 떨어지는 데이터에 대해 더 집중해서 학습하도록 하는 효과를 가져옴.
- 그레이디언트 부스팅
  - 비용함수를 최소화하는 방향
  - 가중치를 조정하는 대신에 모델이 유사잔차(pseudo-residual)를 학습하도록 함.
  - 잔차가 큰 데이터를 더 집중적으로 학습하는 효과를 가져옴.
- 확률적 그레이디언트 부스팅
  - 각 라운드마다 레코드와 열을 재표본추출하는 것을 포함한 부스팅의 일반적인 형태
  - 랜덤포레스트와 유사(매 단계마다 데이터와 예측변수를 샘플링하는 것)

6.4.2 XG 부스트

XG부스트 (XGBoost) : 확률적 그레이디언트 부스팅을 구현
R에서도 xgboost 패키지 이용
중요 파라미터
- subsample
  - 각 반복 구간마다 샘플링할 입력 데이터의 비율을 조정
  - subsample 설정에 따라 비복원 추출로 샘플링한다는 점만 빼면 부스팅은 마지 랜덤포레스트와 같이 동작
- eta
  - 부스팅 알고리즘에서 a~m~ 에 적용되는 축소 비율을 결정.
  - 가중치의 변화량을 낮추어 오버피팅을 방지하는 효과가 있음.

xgboost를 대출 데이터에 적용하는 과정 (두가지 변수만 고려)

> library(xgboost)
> 
> predictors <- data.matrix(loan3000[, c('borrower_score',
+                                        'payment_inc_ratio')])
> 
> label <- as.numeric(loan3000[,'outcome']) -1
> xgb <- xgboost(data=predictors, label = label,
+                objective = "binary:logistic",
+               params = list(subsample=.63, eta=0.1), nrounds = 100)
[1]	train-error:0.366333 
[2]	train-error:0.349333 
[3]	train-error:0.338667 
[4]	train-error:0.336333 
[5]	train-error:0.332333 
..............
[98]	train-error:0.251000 
[99]	train-error:0.250000 
[100]	train-error:0.247667 

xgboost는 수식이 포함된 문법을 지원하지 않기 때문에 예측변수는 data.matrix 형태로, 응답 변수는 0/1 형태로 변형해서 사용해야함.

objective 파라미터는 문제가 어떤 종류인지 설정하기 위한 것.

predict 함수를 이용한 예측 결과 그래프

pred <- predict(xgb, newdata = predictors)
xgb_df <- cbind(loan3000, pred_default=pred>.5, prob_default=pred)
ggplot(data=xgb_df, aes(x=borrower_score, y=payment_inc_ratio,
                        color=pred_default, shape=pred_default))+
  geom_point(alpha=.6, size=2)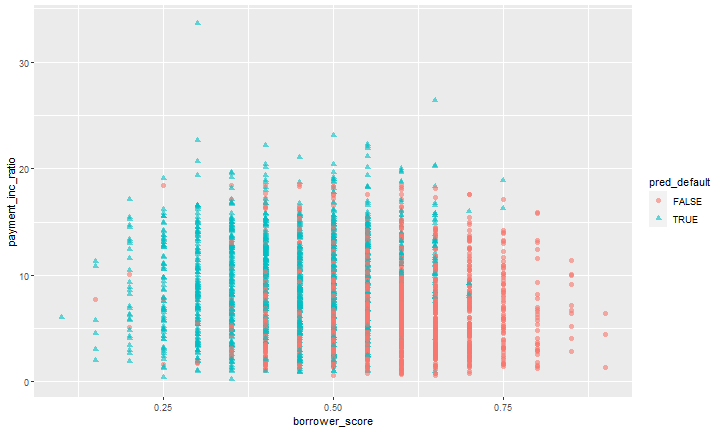

Rplot29

6.4.3 정규화: 오버피팅 하기

xgboost 함수를 무작정 사용할 경우, 학습 데이터에 오버피팅되는 불안정한 모델을 얻을 수 있음
오버피팅 문제
- 학습 데이터에 없는 새로운 데이터에 대한 모델 정확도가 떨어짐
- 모델의 예측 결과에 변동이 매우 심하고 불안정한 결과가 나옴
회귀방정식도 너무 많은 변수를 고려하면 잘못된 예측 결과가 나옴.
xgboost도 예측변수들을 까다롭게 걸러내는 과정이 필요함.

대출 데이터에서 모든 변수를 고려해 xgboost 학습 시킨 결과

> predictors <- data.matrix(loan_data[, -which(names(loan_data) %in% 'outcome' )])
> label <- as.numeric(loan_data$outcome)-1
> test_idx <- sample(nrow(loan_data), 10000)
> xgb_default <- xgboost(data = predictors[-test_idx, ],
+                        label = label[-test_idx],
+                        objective = "binary:logistic", nrounds = 250)
[1]	train-error:0.000000 
[2]	train-error:0.000000 
[3]	train-error:0.000000 
[4]	train-error:0.000000 
............
[246]	train-error:0.000000 
[247]	train-error:0.000000 
[248]	train-error:0.000000 
[249]	train-error:0.000000 
[250]	train-error:0.000000 
> 
> pred_default <- predict(xgb_default, predictors[test_idx,])
> error_default <- abs(label[test_idx] - pred_default) > 0.5
> xgb_default$evaluation_log[250, ]
   iter train_error
1:  250           0
> 
> mean(error_default)
[1] 1e-04
> 

위의 결과는 오버피팅의 결과다.

이 부스팅 모델이 새로운 데이터에는 잘 맞지 않는다.

부스팅 오버피팅 방지하는 방법 중 subsample이나 eta외에 정규화 방법도 있음.

정규화하기 위한 두 파라미터
- alpha : 맨하탄 거리
- lambda : 유클리드 거리
이 파라미터를 크게하면 모델이 복잡해질수록 더 많은 벌점을 부여함. 결과적으로 트리의 크기도 작아짐.
lambda 값이 1000일 경우

> xgb_penalty <- xgboost(data = predictors[-test_idx,],
+                        label = label[-test_idx],
+                       params = list(eta=.1, subsample=.63, lambda=1000),
+                       objective = "binary:logistic", nrounds=250)
[1]	train-error:0.000028 
[2]	train-error:0.000028 
[3]	train-error:0.000000 
[4]	train-error:0.000000 
............
[249]	train-error:0.000000 
[250]	train-error:0.000000 
> 
> pred_penalty <- predict(xgb_penalty, predictors[test_idx,])
> error_penalty <- abs(label[test_idx] - pred_penalty) > 0.5
> xgb_penalty$evaluation_log[250,]
   iter train_error
1:  250           0
> 
> mean(error_penalty)
[1] 1e-04
  

ntreelimit 파라미터 제공
- 예측을 위해 첫 i개의 트리 모델만을 사용하는 것을 가능하게 함.
- 이를 통해 예측을 위해 사용하는 모델의 개수에 따른 표본 내 오차율과 표본 밖 오차율을 더 쉽게 비교

6.4.4 하이퍼파라미터와 교차타당성검사

xgboost 함수에는 하이퍼파라미터 존재
이를 해결하기 위해 교차 타당성검사 활용
교차 타당성 검사
- K개의 서로 다른 그룹(폴드)으로 랜덤하게 나눔
- 폴드마다 해당 폴드에 속한 데이터를 제외한 나머지 데이터를 가지고 모델을 학습
- 폴드에 속한 데이터를 이용해 모델을 평가
이는 결국 표본 밖 데이터에 대한 모델의 성능을 보여줌.
설정한 하이퍼파라미터 조합마다 오차의 평균을 계산하여 전체적으로 낮은 평균 오차를 갖는 최적의 하이퍼파라미터 조합을 찾음.

xgboost 함수의 파라미터 활용

eta : 축소 파라미터
max_depth : 트리의 최대 깊이 ( 트리의 뿌리에서 잎 노드 까지 최대 깊이를 의미), 기본값은 6
폴드들과 테스트할 파라미터 값들의 리스트를 설정

N <- nrow(loan_data)
fold_number <- sample(1:5, N, replace = TRUE)
params <- data.frame(eta=rep(c(.1, .5, .9), 3),
                     max_depth = rep(c(3,6,12), rep(3,3)))
  
error <- matrix(0, nrow=9, ncol=5)
for(i in 1:nrow(params)){
  for(k in 1:5){
    cat('Fold', k, 'for model', i, '\n')
    fold_idx <- (1:N)[fold_number == k]
    xgb <- xgboost(data=predictors[-fold_idx,], label=label[-fold_idx], 
                   params = list(eta = params[i, 'eta'], 
                                 max_depth = params[i, 'max_depth']),
                   objective = "binary:logistic", nrounds=100, verbose=0)
    pred <- predict(xgb, predictors[fold_idx,])
    error[i, k] <- mean(abs(label[fold_idx] - pred) >= 0.5)
  }
}

rowMeans 함수를 이요해 다른 파라미터 조합 간의 오차율 비교

avg_error <- 100 * round(rowMeans(error), 4)
cbind(params, avg_error)

참고 : 해당 포스트의 내용은 O’REILLY 시리즈 데이터 과학을 위한 통계 ( 피터 브루스 & 앤드루 브루스 저, 한빛미디어 출판) 도서를 요약한 내용입니다.